Speech Pitch Detection Using Modified AMDF

The use of average magnitude difference function (AMDF) comes with the problem of double pitch in noisy conditions. Double pitch is the scenario where twice the pitch is rather returned instead of the desired pitch period. A couple of ways are used to reduce the prevalence of double pitch detection.Suppose the received signal at the microphone is given as:

$y[n]= s[n] + \nu[n]$

where $s[n]$ is the desired speech signal and $\nu[n]$ is i.i.d zero mean Gaussian noise. The AMDF algorithm proceeds on a frame by frame basis. Suppose a frame of length N is available,such that $0 \le n \le N-1$ . Then the AMDF function is defined as:

$AMDF[k] = \frac{1}{N-k-1} \sum\limits_{n=0}^{N-k-1} \left|y[n] - y[n+k]\right|, ~~ 0 \le k \le N-1$

The pitch is found using:

$P[n] = \underset{k}{argmin} ~~AMDF[k]$

The first approach to reduce the effect of noise in moving the pitch period to the double, is the use of high resolution AMDF, denoted HRAMDF. HRAMDF is defined as:

$HRAMDF[k] = \sum\limits_{n=\frac{\frac{N}{2}-k}{2} +1}^{\frac{\frac{N}{2}-k}{2} +\frac{N}{2}} \left|y[n] - y[n+k]\right|, ~~ 0 \le k \le \frac{N}{2}-1$

The pitch is found using:

$P[n] = \underset{k}{argmin} ~~HRAMDF[k]$

The main difference between AMDF and HRAMDF are that, in HRAMDF, all time scales are averaged over the same number of samples. This reduces the effect of the falling trend and just a minimal effect on the double pitch problem. A further modification is used in the circular AMDF, which is defined as:

$CAMDF[k] = \sum\limits_{n=0}^{N-1} \left|y[n] - y[{\text mod} {(n+k,N)}]\right|, ~~ 0 \le k \le N-1$

The pitch is found using:

$P[n] = \underset{k}{argmin} ~~CAMDF[k]$

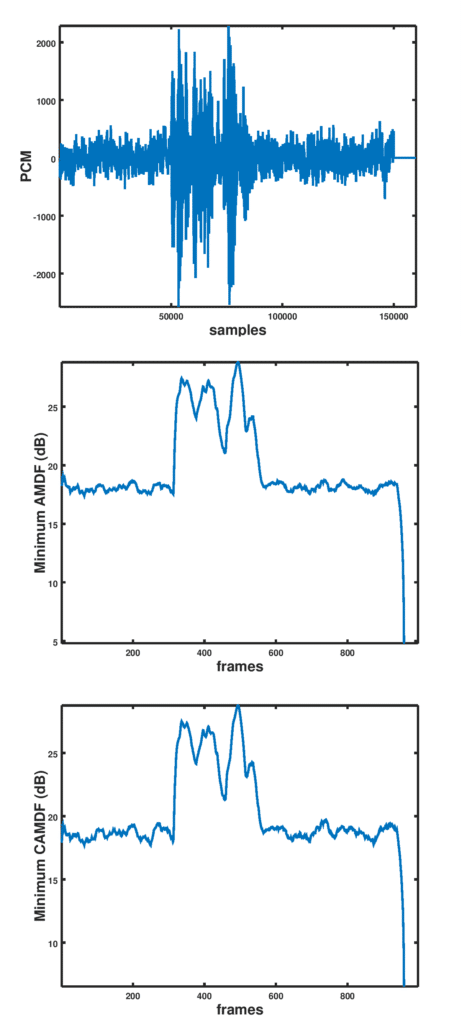
A smoothening function can be applied to $P[n]$ to remove spurious noise. A sample performance of AMDF is shown in Figure 1 below:

Figure 1: Pitch detection in speech using AMDF and CAMDF

The differences in the two approaches are subtle and not very noticeable.

VOCAL Technologies offers custom designed solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!

More Information

Complete Communications Engineering

Speech Pitch Detection Using Modified Average Magnitude Difference