Second Order Digital Equalizers

Tunable digital equalizers are used to adjust gains at specific frequencies whiles maintaining the gains at all other frequencies. Second order equalizers can be used for real time signal enhancement procedures to improve speech quality adjusting the magnitude responses of specified frequencies.

Consider a first order analog transfer function in Laplace domain:

$H(s) = \frac{s + \alpha \beta}{s + \alpha} = \frac{s}{s + \alpha} + \beta \frac{\alpha}{s + \alpha}$

The transfer function can be rewritten as:

$H(s) = \frac{1}{2} (1+\gamma(s)) + \frac{\beta}{2} (1-\gamma(s))$

where $\gamma(s) = \frac{s-\alpha}{s + \alpha}$ . Then, using the bi-linear transformation of $s = \frac{2}{T} \frac{z-1}{z+1}$ , the realized digital filter becomes:

$H(z) = \frac{1}{2} (1+\gamma(z)) + \frac{\beta}{2} (1-\gamma(z))$

$\gamma(z) = - \frac{z^{-1} -\hat{\alpha}}{1-\hat{\alpha} z^{-1}}$

where $\hat{\alpha} = \frac{\frac{2}{T}-\alpha}{\frac{2}{T}+\alpha}$ where $T$ is the integration step of the trapezoid rule.\\Now suppose we make a further transformation of

$z^{-1} \rightarrow -z^{-1} \frac{z^{-1} + \delta}{1 + \delta z^{-1}}$

where $\delta = - \cos{\omega_{\delta}}$ with $\omega_{\delta}$ being the desired center frequency of the bin to be adjusted. This will lead to

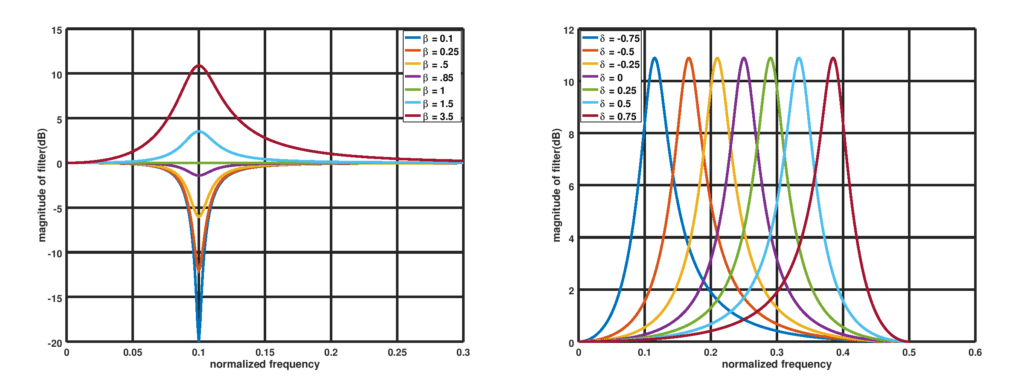
$\gamma(z) = \frac{z^{-2} + \delta(1 + \alpha)z^{-1} +\alpha}{1 + \delta(1 + \alpha)z^{-1} +\alpha z^{-2}}$

Figure 1: Low frequency gain adjusted by varying $\beta$ with $\alpha = 0.85, \delta = -0.80902$ on the left and varying $\delta$ with $\alpha = 0.81, \beta = 3.5$ on the right

VOCAL Technologies offers custom designed solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!

Complete Communications Engineering

Second order digital equalizers