Maximum Likelihood Voice Activity Detector

In almost all online sound signal processing, a voice activity detector, VAD, is utilized to limit the the use of the expensive computational time to frames which have high likelihood of acoustic signal presence. There are various means of detecting the presence or otherwise of an acoustic source. Most algorithms invariably end up being a pseudo measure of the energy levels present in the frames. We present an approach based of hypothesis testing by using the stochastic characteristics of noise and the acoustic signals. Our approach ends up limiting the need for keeping track of the signal to noise ratio.

Consider an acoustic signal impinging a microphones. suppose the signal at a microphone, $x$ , can be denoted as:

$x(t) = s(t) + \nu(t)$

where both nonlinear attenuation and delay have been subsumed without any loss of generality in $s(t)$ ,the source signal, and $\nu_i(t)$ is noise. Both $s(t)$ and $\nu (t)$ are zero mean ergodic processes. The frequency domain representation becomes:

$X[k] = S[k] +N[k], \mathbb{E}{\left[\frac{1}{N} \sum\limits_{k=1}^M N[k]\right]} \sim \mathbb{N} (0,\sigma_n^2)$

Define the following admissible hypothesis:

$H_0: X[k] = N[k]$

$H_1 : X[k]= S[k] + N[k]$

It can be shown that the log likelihood ratio will obey:

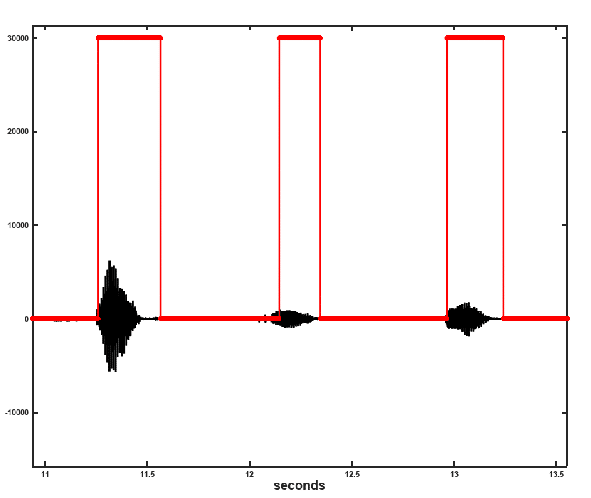
$\frac{1}{N} \sum\limits_{k=1}^M |X[k]|^2 \underset{H_1}{\overset{H_0}{\lessgtr}} \frac{\log{\left( \frac{1}{N} \sum\limits_{k=1}^M |X[k]|^2 \right)}-\log{\sigma_n^2}}{\frac{1}{\sigma_n^2}-\frac{1}{\left( \frac{1}{N} \sum\limits_{k=1}^M |X[k]|^2 \right)}}$

The value of the noise variance, $\sigma_n^2$ , can be computed at the initiation point and may also be updated intermittently or otherwise. The performance using a one-off static noise variance estimate is shown in Figure 1 below.

Figure 1: Performance of maximum likelihood based VAD

VOCAL Technologies offers custom designed direction of arrival estimation solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!\end{document}

Complete Communications Engineering