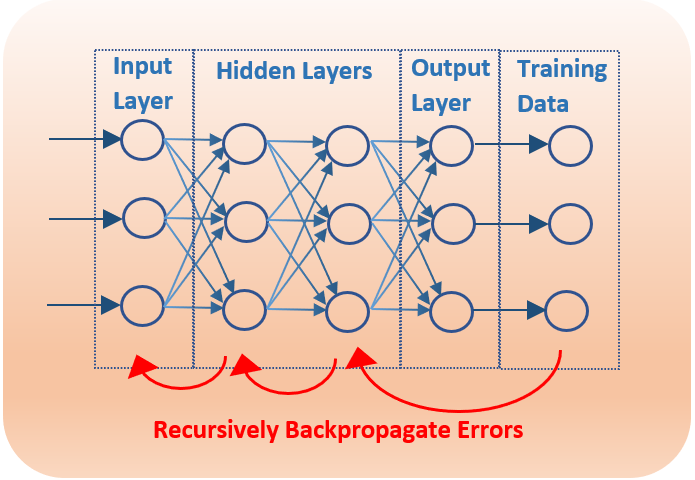
Deep Neural Networks (DNN) can be applied to speech enhancement, speech coding and speech recognition tasks. The vanishing gradient is a common problem of DNN for these and other applications. The core of the learning algorithm of a neural network is the gradient descent algorithm. The DNN parameters are updated by an amount that is proportional the partial derivative of the cost function. Backpropagation of the error signals from the upper layers (layers near the output) via the chain rule are used to update the lower layers (layers near the input). Since the values of non-linear activation functions quickly transition between 0 and 1, as the number of layers increases, the gradient becomes smaller (vanishing) with each recursive update to the next layer. This can result in the lower layers failing to be updated during the training phase.
Rectified Linear Units (ReLU) and skip connections are two popular techniques to resolve the vanishing gradient problem. ReLU activation function is g(x) = max(0,x). Between 0 and 1, this function has linear properties which avoid the quick transitions of non-linear functions, reducing the decay rate of the gradient across layers. ReLU is still a non-linear function as values below zero are clamped to 0, which helps to provide non-linear modeling of the neural network. Residual skip connections use gradients not only from the previous layer, but from earlier layers as well. This has the effect of skipping the layers that cause the vanishing gradient.