The normalized least mean squared (NLMS) algorithm is a specialized version of the least mean squared method which attempts to account for signals with time-varying average power. This is useful for applications whose parameters are nonstationary, such as speech. Using the NLMS algorithm allows for the filter taps to be updated in such a way that they reflect the changes in the energy level of the signal, which improves the convergence behavior of the algorithm. Because nonstationary signals have time-varying average power, NLMS can be a more ideal choice than LMS for certain applications such as echo cancellation, where the eigenvalue spread of the autocorrelation matrix R may be large.
Changes in the adaptive coefficients in a stationary state are dependent on two factors: step size, and signal energy. Hence, in NLMS the step size is reduced (normalized) in cases where the signal energy influences the filter tap weight coefficients in a harmful way. When compared to conventional LMS, NLMS is relatively less susceptible to problems caused by eigenvalue spread because of its ability to adjust its step-size each based on the signal energy.
Recall the basic iterative procedure for the conventional LMS algorithm below. The filter coefficients H are computed as follows:
This formula can be modified to NLMS with the following adjustment:
where is a small valued constant,
and
is some chosen value with a convergence bound
In cases where signal energy
is very small, a value of
may be used. The
constant controls the rate of convergence, as well as the amount of misadjustment in the algorithm. A typical application may use a
value of
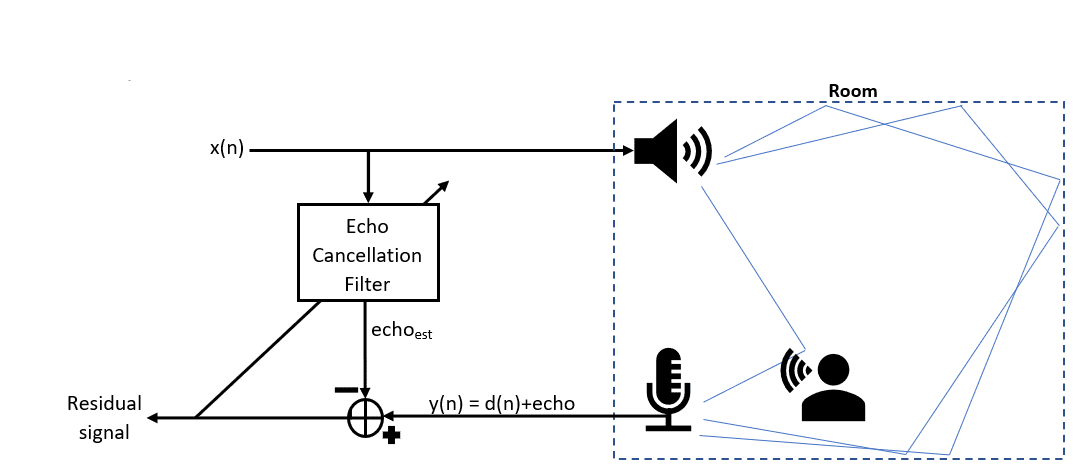
NLMS is a common algorithm for adaptive echo cancellation applications. A block diagram displaying this application is shown in the figure below.