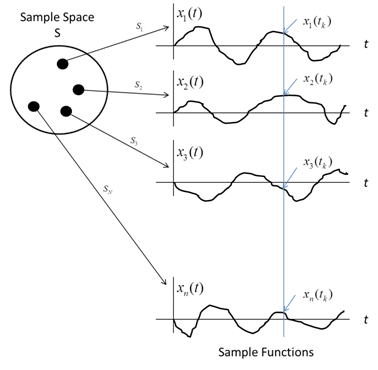
The characterization of random signals is of paramount interest in the statistical analysis of any communication system. Random signals can include electrical noise, audio signals, television signals, and even computer data. These random signals are functions of time (discrete or continuous) and are random in the sense that before conducting an experiment it is not possible to precisely predict the waveform (or function of time) that will be observed. Therefore when describing random signals one must refer to a sample space ‘S’ from which they originate. The sample space can be viewed as a bin from which waveforms are randomly drawn. Each sample point in the sample space (or bin) then corresponds to an individual waveform. This sample space or ensemble comprised of functions constitutes what is known as a random or stochastic process.
This concept is illustrated in Figure 1 below where each sample point in the sample space corresponds to an outcome Sn(n=1, 2, … N) of the random experiment. Each sample point is then assigned a function of time and each function of time is called a realization of the random process.
Figure 1: Illustration of a sample space for a random process
In order to quantify the statistical model of a stochastic process, an underlying probability distribution is defined over an appropriate class of sets in the sample space. For instance, consider a fixed time during the observation interval in the figure above, the set of numbers {x1(tk). x2(tk). x3(tk). …, xn(tk)} represents a random variable. Therefore, for every instance of time, there is an indexed ensemble of random variables across the sample functions. A random process is usually denoted by the function X(t).
An example of a statistical property of a random process is its mean. The mean of a process at time tk can be given by the expected value of the random variable observed at that time.
Where 
is the probability density function of the process at time tk. The process is known as stationary to first order if
forall t
That is the mean of the process does not vary with time.
Determining the underlying statistical properties of random signals is extremely useful. A measured waveform such as an audio signal cannot be completely known before it is observed (i.e. it is not deterministic). Audio signals are typically accompanied by the presence of additive noise, andoften must be filtered. Building a filter based on one realization of a random process may not work very well. A filter based on the features of the random process as a whole (all possible realizations) can be much more effective. Determining the features or statistical quantities of a random process is therefore extremely important and stochastic modeling is a tremendously useful tool.
More Information
References
[1] SHaykin and M Moher, Communication Systems, 5th ed. (New Jersey: John Wiley & Sons Inc., 2009).