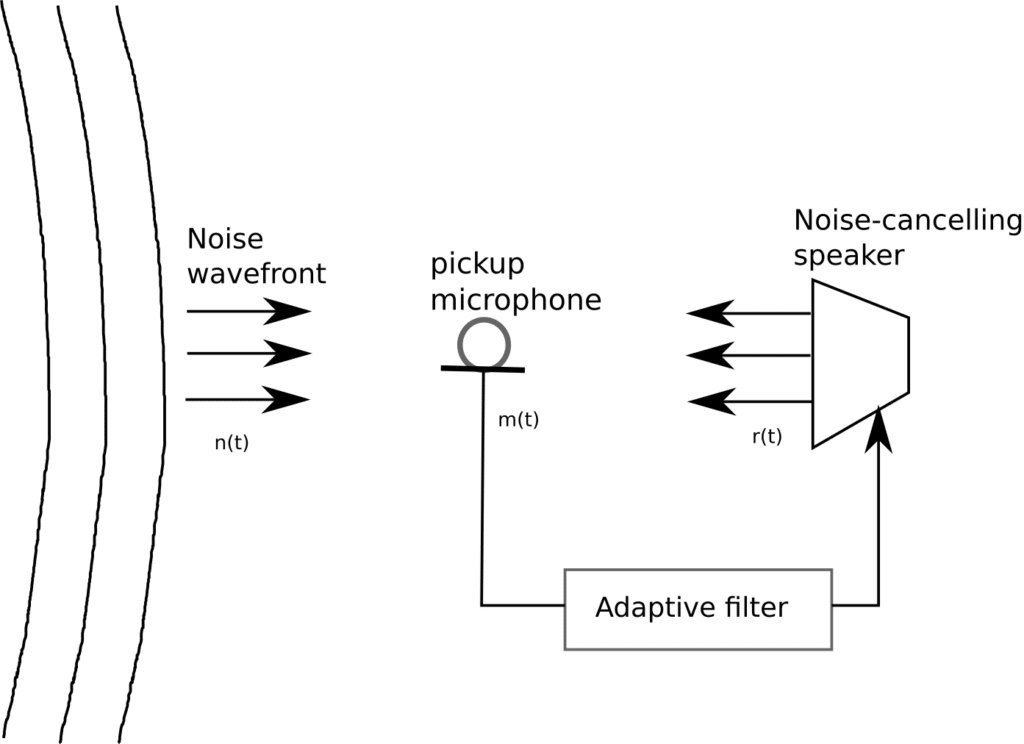
In many industrial settings, high levels of unwanted acoustic noise are prevalent. Active noise cancellation in a procedure to destructively interfere with the acoustic wavefront of the noise signal and attenuate it as. An active noise system will comprise of at least one microphone and one speaker to feedback the destructive signal for canceling.
Consider a the scenario depicted in Figure 1:
Figure 1: Single microphone active noise cancellation
From Figure 1, the prediction error becomes
The objective then is to minimize the energy of the error signal . Due to the physical distance between the source and the pickup microphone, the noise canceling speaker should have an
step look ahead predicted signal based on past observations. The noise signal can be modeled as an ARMA signal such that
where is a zero mean Gaussian process and independent of
. The
estimate is then given as
An extended Kalman filter can be employed to compute the expected signals.
VOCAL Technologies offers custom designed solutions for robust beamforming, voice activity detector, acoustic echo cancellation and noise suppression and active noise cancellation. Our custom implementations of such systems are meant to deliver optimum performance for your specific task. Contact us today to discuss your solution!