It seems natural that the recovered speech can be further utilized enhancing the new noisy speeches. When the Wiener filter output is used to design a higher performance Wiener filter, we refer the process as Iterative Wiener filtering. This small article describes the practical use of such an idea in signal enhancement.
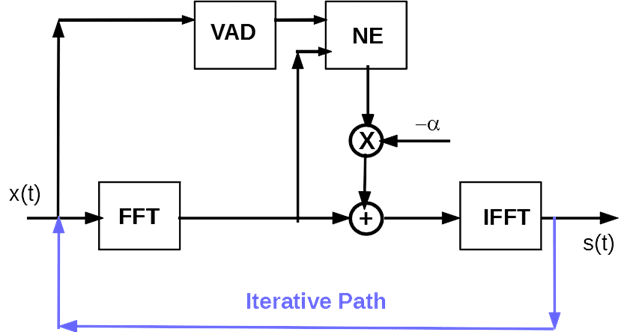
Figure 1 shows the iterative noise reduction process. The standard noise reduction step produces an output s(t). This output is fed back through the iterative path to the beginning of the noise reduction unit again. The feedback signal is then used to achieve a more accurate noise estimation. The performance will be increased with each iteration. The process can go on until non further perceptual improvement is observed.
With each iteration, the nature of the noise may change. For example, the original noise to the noisy speech may be additive and wide band. After one iteration, the residual noise becomes musical and tonal. Therefore, different sets of parameters must be chosen for different iteration.
A commonly used modification is the following,
where , which is often referred to as the over-subtraction factor, and
, which defines the noise floor, and ɣ is a new parameter that controls the transition sharpness.