Echo cancellation solutions are most often based on a linear FIR adaptive filtering approach. In fact all real-life echo paths are IIR filters and their approximate representation by FIR filters is dictated by conceptual simplicity (as only B-type filter coefficients have to be taken into account, as opposed to B and A-type coefficients needed for IIR filters) and FIR filter stability property.
This conceptual simplicity has its notable cost: even a modest approximate model of the real-life echo path has a large number of filter coefficients. A very good approximation of the same real-life echo path would have much smaller number of coefficients, B-type and A-type combined. Therefore, this question can be asked:
- With this additional cost in terms of number of FIR coefficients (i.e., B-type coefficients; A-type coefficients is reduced to 1), why do most implementations of echo canceller solutions, both for line and acoustic echo cancellation, use FIR adaptive filters and not IIR adaptive filtering?
- Actually, the same question can be asked in the context of other applications of adaptive filtering, such as adaptive noise control, active noise and vibration control, to mention just a few.
Based on the properties of FIR filtering, the answer is quite straightforward: FIR filters, contrary to IIR filters, are inherently stable. Consequently, the FIR filter transfer function has only zeroes. This property of FIR filters contrasts with IIR filters: the transfer functions do have poles and for some values of A-type coefficients these poles can be outside of the unit circles, thus causing the IIR filter instability (cf. Ref.[1,2]). Although the adaptive FIR filter can become unstable, but this instability relates solely to the adaptation process. By choosing the right adaptation step the adaptive FIR filter does not produce the unbounded output for the bounded input (here we are referring to the BIBO stability).
In the case of IIR filters, there are at least two type of instability: the inherent instability of the IIR filters (with static coefficients) plus the instability related to the adaptation process (i.e., when the coefficients change in the adaptation process). These reasons caused the research and development of adaptive filters to focus mostly on the FIR filters and, as a result, FIR adaptive filters are much better understood and refined (cf. Ref. [3]).
However, the IIR adaptive filters do have merit, and there are many practical applications which take advantage of the smaller number of coefficients required to adequately model the system that the filter is to approximate or mimic as per LMS criterion. Of course, their implementations are more complex as additional precautions have to be taken in order to control the IIR stability in the course of the adaptation process.
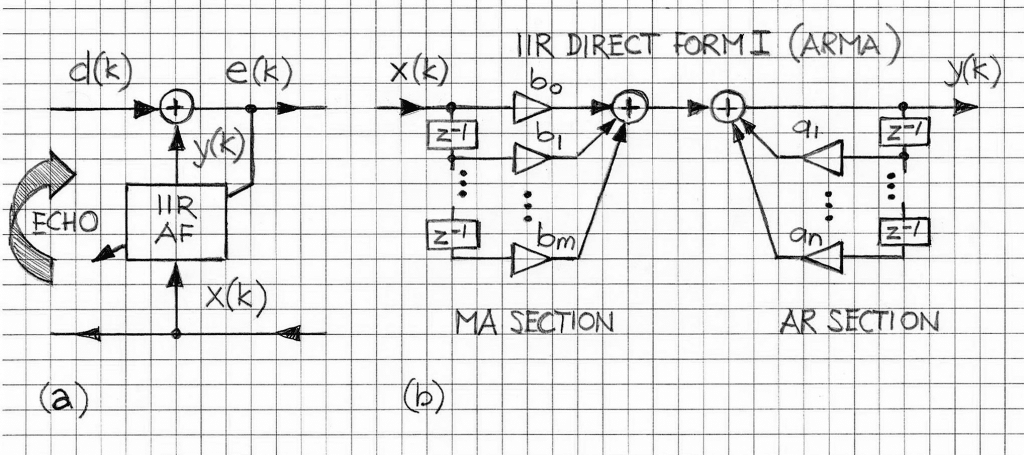
Figure 1 provides an outline of the IIR filter-based echo canceller block diagram. The IIR filter structure used there is Direct Form I, corresponding exactly to Equation 1 (autoregressive moving average, ARMA, model). The IIR adaptive filter-based echo cancellation solution is a high-level view; (a) IIR adaptive filter of the echo canceller under consideration; (b) structure of the IIR filter (as employed in block IIR AF of (a); the structure of Direct Form I with separate Moving Average (MA) section and Autoregressive (AR) section )
Equation 1 reflects the standard ARMA model of the IIR filter. The adaptation process now involves both B coefficients (B = [b0, b1, …, bm], bj=bj(k), j=0,1,…,m) and A coefficients (A = [a1, a2, …, an], ai=ai(k), i=1,2,…,n .) , and opposed to the FIR filter case, which is limited to B coefficients, by definition.
In the case of the most popular adaptive algorithm (i.e., LMS algorithm), the adaptation formula for W = [A, B]T is given by the following:
W(k+1) = W(k) + ΛΨ(k)e(k), (2)
where
e(k) = d(k) – XT(k)WΨ(k), (error signal) (3)
Λ =diag [μ1 … μn ρ0 … ρm], (adaptation step matrix) (4)
X(k) = [y(k-1), …, y(k-n),x(k), x(k-1),…,x(k-m)]T . (5)
Although Equations 1-5 are direct extensions of the FIR adaptive-filter case, details regarding the choice of the adaptation step matrix Λ and control of the adaptation process stability make the IIR adaptive filtering more complex despite the overall smaller number of coefficients to adapt.
VOCAL’s implementations of the echo cancellation designs are based on the full-band and sub-band NLMS adaptive algorithm. An IIR version of the full-band NLMS adaptive algorithm can be added as a custom offering, if required.
More Information
References
- Theory and Design of Adaptive Filters, Treichler, R.R., Johnson Jr, C. R., Larimore, M.,G., Series: Topics in Digital Signal Processing, John Wiley and Sons, 1987
- Adaptive IIR Filtering, Steward, B., University of Strathclyde, Glasgow, March 2006
- A new adaptive recursive RLS-based fast-array IIR filter for active noise and vibration control systems, Montazeri,A. and Poshtan, J., Signal Processing 91(2011) 98–113; Elsevier