There are several methods used to de-reverberate speech distorted in the acoustic part of the (tele)communication channel. Here we intentionally limit the scope to de-reverberation methods that use channel inversion and equalization approach. There are three variants (and we will call them methods) of this approach.
- Direct Inverse Method
- MMSE/LS
- MINT
The reverberation effect occurring in room or other confined acoustical spaces significantly contributes to speech degradation as received at the other end of communication channel (the “other end” means a listener in the same room or at a remote end, and then the “channel” includes acoustic field as well as the telecommunication channel). In the latter case, distinct from the reverberation, there are two other factors significantly affecting speech degradation, noise and echo.
Apart from affecting communication between two human users of the (tele)communication channel, the reverberation effect adversely affects Automatic Speech Recognition (ASR) performance if on the receiving end there is a machine equipped with speech recognition algorithms.
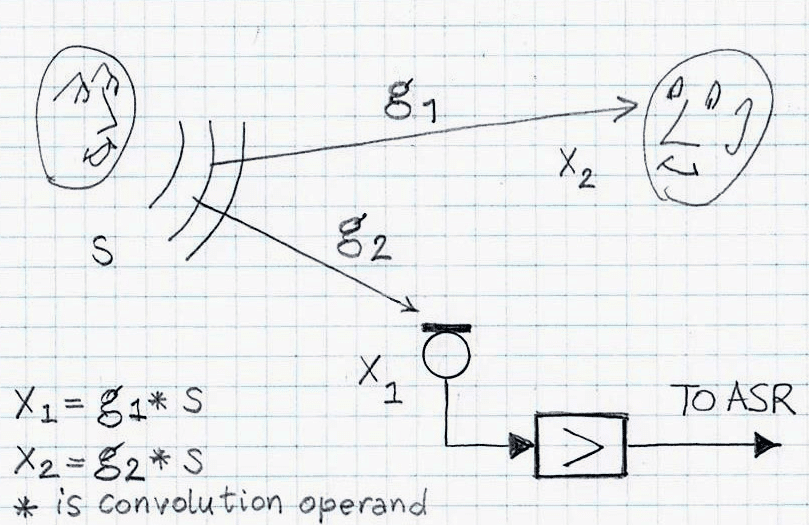
Direct inverse Method (DIM) is the most straightforward one out of these three methods. It assumes that the impulse response of the acoustic channel is already known. Figure 1 illustrates two common examples of the acoustic channel: talker-to-listener channel and talker-to-microphone-to-ASR channel where s is the input, x is the observed signal at the output (i.e., the signal heard by the listener or the signal captured by the microphone).
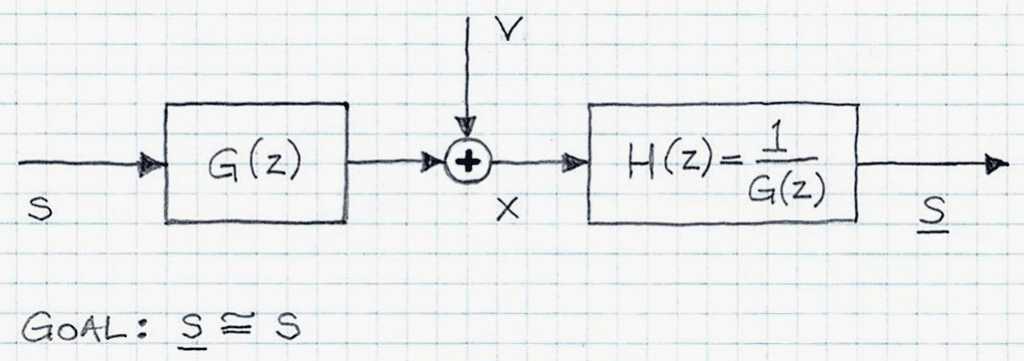
Figure 2 depicts the idea of dereverberation via direct inversion (a.k.a., zero-forcing) method. In this approach, it is assumed that the channel impulse response (cf. Figure 1; g1 or g2, depending on specifics of the acoustic scene) is known beforehand. Note that if the impulse response is not known, it can be estimated based on the unprocessed (meaning, unequalized) response data x1 or x2, taken at the beginning of the acoustic session.
The dereverberation transfer function H(z) is given by:
where G(z) is the z-transform of the g(n) (where g(n)=g1(n) or g(n)=g2(n), depending on the actual acoustic setup) has been estimated separately.
This straightforward relationship (i.e., Eq. 1) implies that the system G(z) has to be a minimum-phase system (i.e., all its poles and zeros have to be within the unit circle in the z-domain) as only then the equalizing system H(z) will be stable and causal. While in many cases transfer functions are of minimum-phase (for example in Circuit Theory, when a graph of the linear circuit network is plane then the transfer function of that circuit transfer function is of minimum-phase), this is not the case in the case of the linear system represented by acoustic reverberation impulse response, where in addition to the direct sound, there are many sound reflections captured and embedded in the impulse response. In short, in the case of room acoustics where the sound reflections cannot be ignored, the transfer function of the room response is never of minimum-phase.
In order to produce acceptable “inverse” system, approximations have to be made and in general they are sensitive to numerical errors thus may become numerically unstable. This and other reasons make the direct inversion approach to de-correlation not a preferable real-time solution.
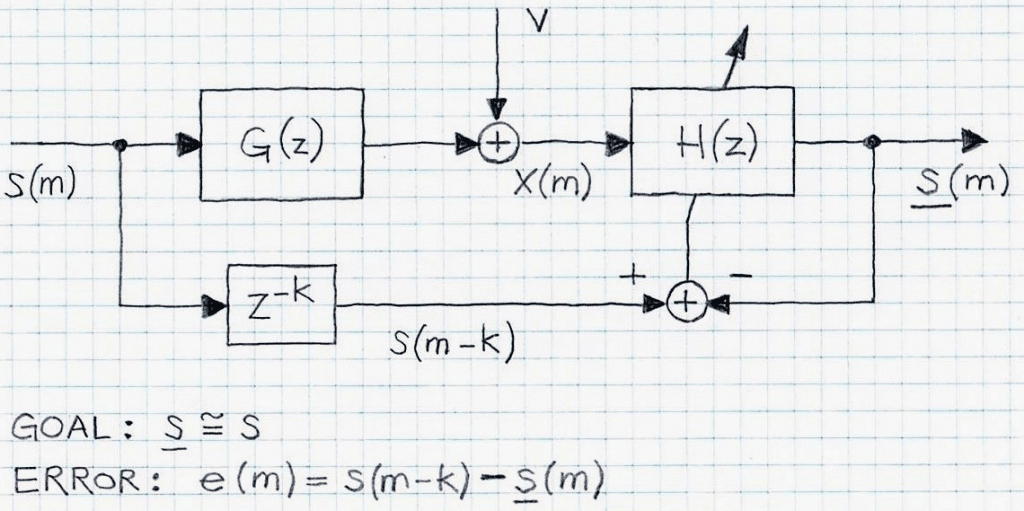
Another approach to the de-reverberation is based on methods employing the minimization of the mean square error and least-squares (MMSQ/LS). Figure 3 illustrates the block diagram depicting this approach. The de-reverberation/equalization filter h (with H(z) = Z(h(m))) is estimated by minimizing one of two measures of “distance” between s(m)(input) and s(m) (output), namely
the MMSE measure
MMSE(e) = E[e2(m)] (2)
where E[.] denotes mathematical expectation operation or the LS measure
where M is the number of observed samples of the respective signals, and the error signal is defined as
e(m) = s(m – k) – s(m) = s(m – k) – h(m) * x(m) (4)
where * denotes convolution.
(Note that for finite and ergodic series, both measures produce equivalent results).
Therefore, the estimations of the de-reverberation filters are
hMMSE = arg h min (MMSE(e)) (5)
and
hLS = arg h min (LS(e)) (6)
With that in mind, we can observe that both tasks (as per Eq. 5 and Eq.6) are typical tasks in Estimation Theory and solutions, hMMSE, hLS, can be found via adaptive or recursive algorithms.
It is worth noting that for minimum-phase single-channel systems, both methods, i.e., MMSE/LS method and the directive inverse (or, zero-forcing) method, produce the same results.
The important feature of the MMSE/LS method is that, unlike in the case of the direct-inverse method, access to the reference signal (i.e., s) is a requirement (as Figure 3 implies). It is definitely a limitation of the MMSE/LS method, yet it is still an approach that has practical benefits.
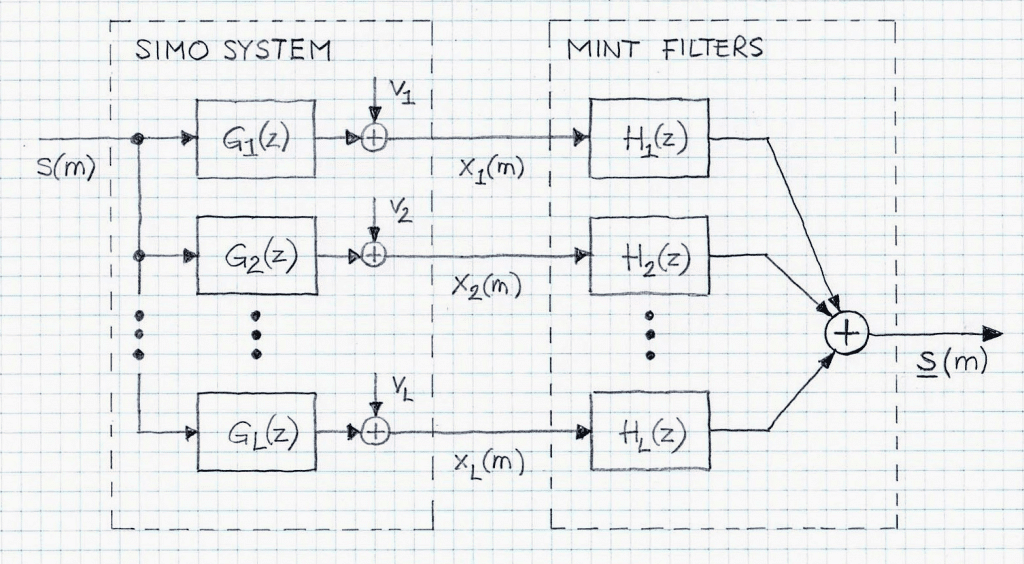
The third approach to de-reverberation, depicted in Figure 4, is called MINT (Multi-channel Inverse Theorem) method. MINT is based on a SIMO system (single-input-multiple-output) which has the notable benefit of not requiring access to the reference signal (s, the input).
The MINT-based equalization is a powerful approach to speech de-reverberation and, if properly implemented, can very efficiently remove traces of reverberation effects from speech. However, there are two caveats regarding the MINT-based equalization:
- The employed channels (i.e., pairs {s,x1}, {s,x2}, …, {s,xL}; cf. Figure 4) should not share common zeroes. If they do, the performance of the method will suffer.
- The method’s sensitivity to computational errors. Therefore, implementations of the MINT-based equalization are computationally intensive as they require increased precision and thus consume more CPU cycles.
VOCAL’s Voice Enhancement solutions include de-reverberation software solutions that have been tested in typical acoustic environment. Custom solutions can be discussed and prototypes can be made provided well-defined specifications are available.