Info Theory Approach To Single Channel Dereverberation

The classical acoustic echo canceler assumes that there is a reference signal which is being utilized to estimate the acoustic impulse response between a loudspeaker and a microphones. In certain situations, this reference signal is unavailable and the problem becomes a blind echo cancellation. Consider the case of a single channel blind de-reverberation problem as illustrated in Figure 1 below:

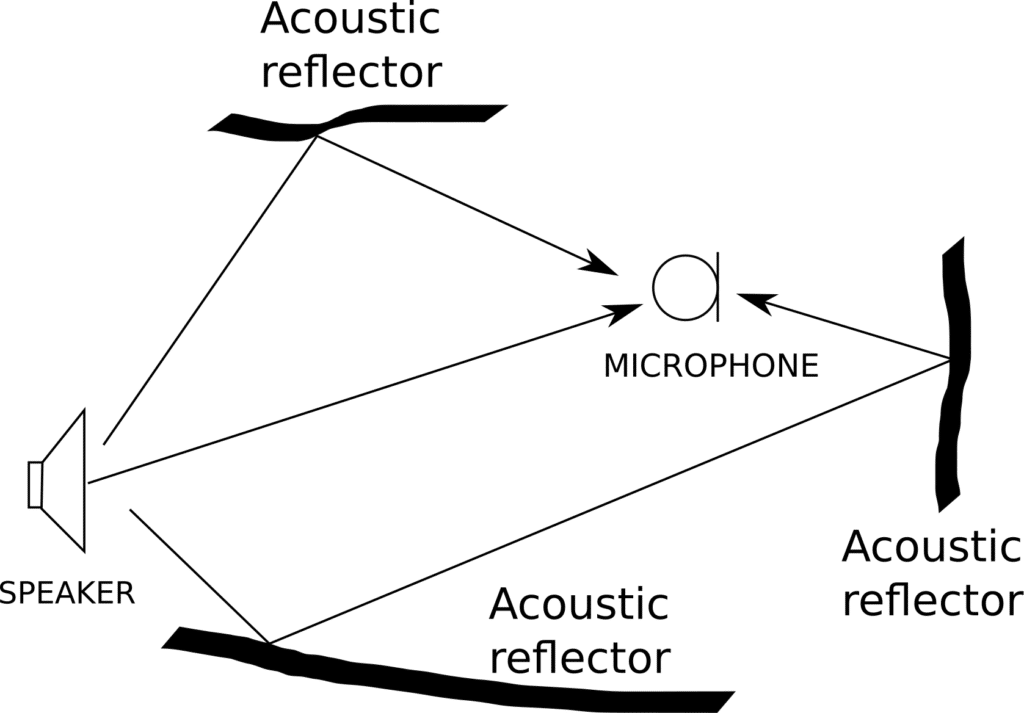
Figure 1: Illustration of room reverberation

It can be seen that the multiple paths have different travel times to the microphone. This will lead to resounding of vocals after the initial direct path vocal. The can be modeled mathematically as:

$x[n]= h_o s[n] + \sum\limits_{k=1}^{L-1} h_k s[n-k] + \nu[n]$

Suppose the received signal is passed through a nonlinear function $z(x[n])$ such that:

$z(x[n]) = \tanh{(\pi \hat{x}[n])}$

where $\hat{x}[n]$ is $x[n]$ normalize by half its dynamic range to make it bounded by $-1 \le \hat{x}[n] \le 1$ . It can be shown that information maximization achieves the same optimum as maximizing the entropy. Since we have applied a nonlinear transformation which leads to a transformation of the density function of $x[n]$ , maximizing the entropy is the same as minimizing the log of the Jacobian $J(z(x[n]))$ , where

$J(z(x[n])) = \frac{\partial z(x[n]) }{\partial s[n]} = (1-z(x[n]) ^2)h_o$

Therefore

$\frac{\partial \log{J(z(x[n]))} }{\partial h_o} = \frac{1}{h_o}-2z[n]s[n]$

Similarly,

$\frac{\partial \log{J(z(x[n]))} }{\partial h_k} = -2z[n]s[n-k]$

An adaptive, recursive least squares approach can then be used to de-reverberate the received signal. The drawback to this approach is the number of iterations required to achieve “reasonable” results, with typical values on orders of 40,000.

VOCAL Technologies offers custom designed solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!

More Information

Echo Cancellation Design

Complete Communications Engineering

Information theoretic approach to single channel dereverberation

More Information