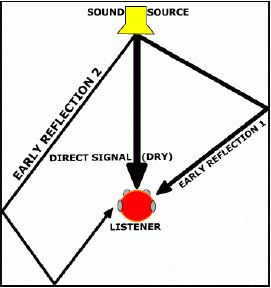
Early reflections are the echoes of a signal that arrive at the microphone within a stretch of about 30ms after the direct sound. Early reflections are direct copies of the direct sound source, rather than diffuse mixtures as are present in the late reflections, or reverberation, or a sound source. They are often visualized as shown in the figure.
Room Impulse Response
In the room impulse response (RIR), the early reflections have a distinct character when compared to the other components. In particular, early reflections are represented by stronger coefficients than late reflections with more space between them. An illustration is shown below:
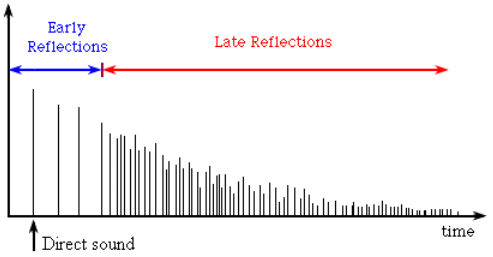
Early reflections add color to the sound source, and are critical for our understanding of distance in a 3D sound field. A signal with strong early reflections will still sound distant, warm, and generally “roomy” despite the complete elimination of late reflection. Therefore, it is imperative that any dereverberation algorithm focusing on voice quality enhancement deal with these distinct early reflections separately.
Observing Early Reflections
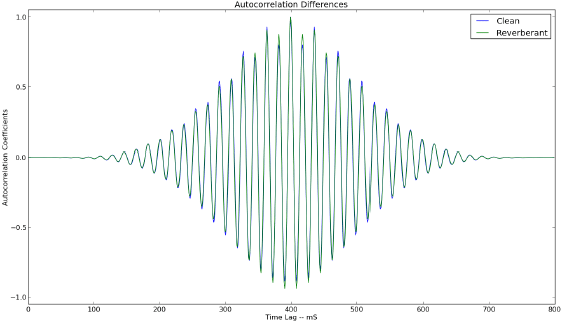
Early reflections show up clearly in the autocorrelation of a speech signal, while they are all but hidden in the spectrogram. The autocorrelation measures how similar a signal is to a time shifted version of itself. Since a speech signal with early reflections contains the direct sound source as well as slightly delayed copies as shown in Figure 1, we will see artificially high sidelobes in the autocorrelation. Consider the autocorrelations of a clean and reverberant stationary voiced segment:
Figure 3: Autocorrelation Difference
As the figure shows, higher side lobes are exactly what we see. Since early reflections are just that, early, the effect becomes less pronounced as time lag is increased. The first sidelobe is the most affected, as expected, while this particular sample has a relatively strong reflection in the third sidelobe. This translates into reverberant autocorrelations having higher energy than clean ones, regardless of the presence of noise.
Dealing with Early Reflections
In a dereverberation algorithm for voice quality enhancement, it is important that early reflections are handled. Here we will discuss the three most widely used methods for dealing with early reflections and thereby reducing coloration and the perception of distance.
Autocorrelation Shaping
Autocorrelation shaping [2] is a method that adaptively modifies the autocorrelation of reverberant speech with early reflections to mold it into something more like clean speech without early reflections. For a given microphone, the autocorrelation of a stationary reverberant speech sample 
is computed as:
Where our block processing notation allows us to use the inner product (•|•) for linear convolution. The correlation shaper will take the form of a filter 
such that the shaped time domain output will take the form:
With the autocorrelation of the desired output denoted as Rdd, we compute the error signal to minimize:
Where W[τ] is a weight to emphasize the importance of the first few peaks which have the greatest distortion due to early reflections. We then obtain the iterative update equation:
Where l represents the update step, and n represents discrete time. The gradient ∇ is given by:
Where Rxy denotes the cross correlation between the reverberant speech and the updating
output. We want to only select lags in a set Τ as to ensure we aren’t cancelling the signal by filtering out the reflection at lag zero, which is the signal itself. Similarly, we can reduce the computational complexity by only focusing on those τ ∈ Τ that contribute substantially to coloration, such as those in some neighborhood of the sidelobe peaks.
Kurtosis Maximization
Early reflection cancellation via kurtosis maximization was developed in [3]. Its low computational complexity and easy to implement algorithm make it one of the most attractive options for dealing with early reflections. It works by adaptively computing filter taps that maximize the kurtosis of the incoming frame’s linear prediction residual. By assuring quasi-stationarity, this filter can be directly applied to the incoming time domain frame thus avoiding the linear prediction synthesis filter. A block diagram is shown below:
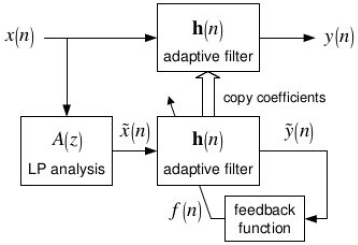Figure 4: Kurtosis Maximization [3]
We can create the linear prediction analysis filter A(z) via Leroux-Gueguen Lattice Filter Recursion as explained in another article on our website. We are building an adaptive filter, therefore we need a reward function to converge towards. As expected, this function is the kurtosis, given by:
Where 
is the output of the adaptive filter applied to the linear prediction analysis filter output 
, and 
represents the sample average. For long term adaptation, these averages should come from an exponential smoother. Since 
, we can take the approximate gradient with respect to 
via:
The update equation for the kurtosis maximization filter is then given by:
To speed up convergence, we typically use a frequency domain implementation of the above discussion. The block diagram remains the same, except each vector is now in the frequency domain. To illustrate how easily this isomorphism is implemented, we consider the frequency domain update equation:
Where m represents the short time frame index, and k represents the discrete frequency bin index. [3] reports that good results were obtained with μ = 0.0004 and H[0, : ] = [1,…,0]Τ . Also in [3], the authors used a Modulated Complex Lapped Transform in place of an FFT. As [4] illustrates, the the MCLT can be implemented by first performing an FFT and then performing a simple subband weighting. Actually, any invertible Gabor transform will work, for instance the Invertible Constant Q, Wavelet Transforms, and the Bark and Mel Transforms.
Conclusion
Early reflections being picked up by a microphone are the principle cause of the perception of distance in an audio signal. Early reflections are modeled as sparse high energy impluses in the room impulse response, and have been shown to appear as extra energy in the first few peaks of the signals autocorrelation. Two methods for early reflection cancellation are autocorrelation shaping, and kurtosis maximization, which can both be implemented adaptively. When combined with a method for dealing with late reflections, a complete dereverberation method is created.
References
[1] A. Oetzmann, D. Mazzoni, Reverb.” Internet: http://audacity.sourceforge.net//manual – 1.2//effects reverb.html,” Jan.28, 2005 [May. 3, 2013].
[2] B.W. Gillespie, L. Atlas, “Strategies for improving audible quality and speech recognition accuracy of reverberant speech,” Proc. IEEE ICASSP, 2003
[3] B.W. Gillespie, H.S. Malvar, and D.A.F. Florencio, Speech dereverberation via maximum-kurtosis subband adaptive filtering, in Proc. Int. Conf. Acoust., Speech, Signal Processing, vol. 6, pp. 3701-3704, 2001.
[4] H.S. Malvar, Fast Algorithm for the Modulated Complex Lapped Transform, Microsoft Corp., Redmond, WA, MSR-TR-2005-2 , 2005.