Uniform Circular Array Uncorrelated Noise SNR Improvements

Uniform circular array uncorrelated noise SNR improvements with delay and sum beamformer. The use of circular array topologies for beamforming as opposed to linear arrays allows the array to remove the $\pi$ look direction ambiguities whilst keeping the advantages of beamforming. Conventional derivations for the signal to noise ratio improvements using delay and sum beamformer is that you get $3dB$ gain for every doubling of the number of microphones being deployed. 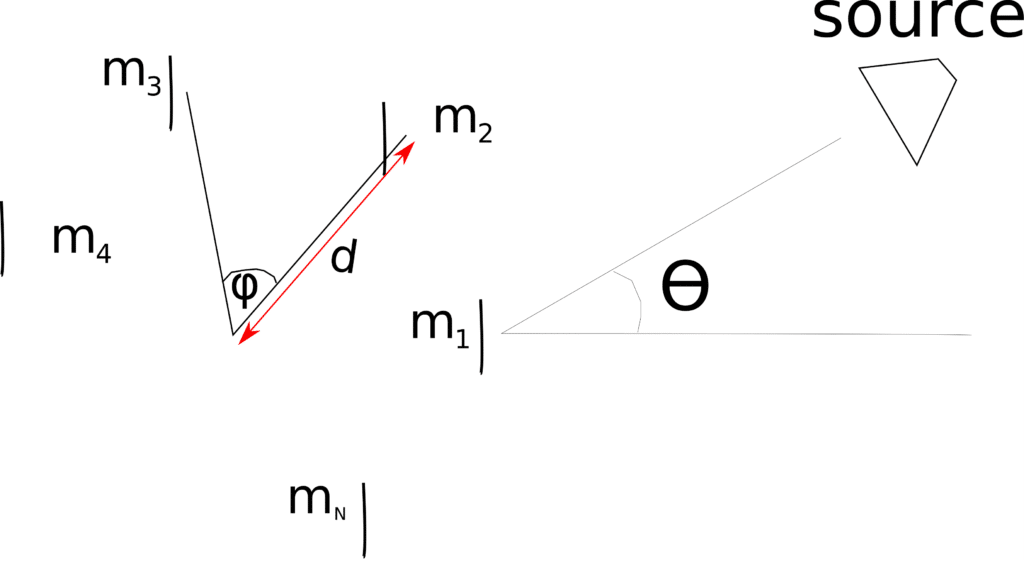This holds $iff$ the noise is not directional or in other words, uncorrelated. We derive the expected SNR gains for uncorrelated noise on UCA microphones and show that it is the same as that for the ULA. Consider a far field source impinging N UCA microphones as shown in Figure 1:

Figure 1: N UCA microphones

Suppose the signal at each microphone $i \in \{1, \cdots, N\}$ is given as

$x_i(w) = s(w) e^{\left(-jw \frac{d}{c} \sin{\left((i-1)\psi - \theta\right)} \right)} + v_i(w)$

where $s(w)$ is the desired speech signal, $\theta$ is the direction of arrival (DOA) of the speech signal with respect to the normal to the axis joining all the microphones, $v_i(w)$ is the uncorrelated noise such that $\mathbb{E}[v_i(w) v_j^*(w)] = 0, i \neq j, \{i,j\} \in \{1, \cdots, N\}$ and $\mathbb{E}[ s(w) e^{\left(-jw \frac{d}{c} \sin{\left((i-1)\psi - \theta\right)} \right)} v_j^*(w)] = 0, \forall {i,j} \in \{1, \cdots, N\}$ .

The input SNR per frequency bin $w$ , denoted $iSNR(w)$ is given as

$iSNR = \frac{\mathbb{E}\left[|s(w)|^2 \right]}{\mathbb{E}\left[\left |v_1(w)\right|^2 \right]}$

where $\mathbb{E}[.]$ is the expectation operator.

After the delay and sum beamformer, the output becomes:

$x(w) = s(w) + \frac{1}{N} \sum\limits_{n =0}^{N-1} v_{n+1}(w) e^{\left(jw \frac{d}{c} \sin{\left((n-1)\psi - \theta\right)} \right)}$

The output SNR per frequency bin $w$ , denoted $oSNR(w)$ is given as

$oSNR = \frac{\mathbb{E}\left[|s(w)|^2 \right]}{\mathbb{E}\left[\left | \frac{1}{N} \sum\limits_{n =0}^{N-1} v_{n+1}(w) e^{\left(jw \frac{d}{c} \sin{\left((n-1)\psi - \theta\right)} \right)} \right|^2 \right]}$

But

$\left| \frac{1}{N}\sum\limits_{n =0}^{N-1} v_{n+1}(w) e^{\left(jw \frac{d}{c} \sin{\left((n-1)\psi - \theta\right)} \right)}\right|^2 =\frac{1}{N^2} \sum\limits_{n =0}^{N-1} |v_{n+1}(w)|^2 + \frac{1}{N^2} \sum\limits_{n =1}^{N} \sum\limits_{m \neq n}^{N} v_{n}(w) v_{m}^*(w) e^{\left(jw\frac{d}{c} \left(\sin{((n-1)\psi-\theta)} -\sin{((m-1)\psi - \theta)} \right)\right)}$

Since by assumption $\mathbb{E}[v_i(w) v_j^*(w)] = 0, i \neq j, \{i,j\} \in \{1, \cdots, N\}$

$\mathbb{E}\left[\left| \frac{1}{N} \sum\limits_{n =0}^{N-1} v_{n+1}(w) e^{\left(jw n \frac{d}{c} \sin{\theta} \right)} \right|^2\right] = \frac{\mathbb{E}[|v_1(w)|^2]}{N}$

This leads to an oSNR of:

$oSNR = N \frac{\mathbb{E}\left[|s(w)|^2 \right]}{\mathbb{E}[|v_1(w)|^2]}$

The SNR improvement, SNRI then becomes:

$SNRI = \frac{oSNR}{iSNR} = N = 2^{\frac{\log{N}}{\log{2}}}$

Thus, if $N$ is increase by a factor of $2$ , the SNRI increases by a factor of $10 \log{2} \approx 3dB$ .

VOCAL Technologies offers custom designed solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!

Complete Communications Engineering