MUSIC (Multiple Signal Classification) Algorithm

MUSIC is a spatial spectrum estimation algorithm based on second order statistics. It attracted intensive studies due to the following perceived advantages.

Capability to handle multiple simultaneous sources
High precision measurement
High spatial resolution
Adjustable to small observable data cases
Possible for real time implementation.

This short paper the basic idea and implementation are described. Its use for resolving multiple sound sources with antenna array is discussed.

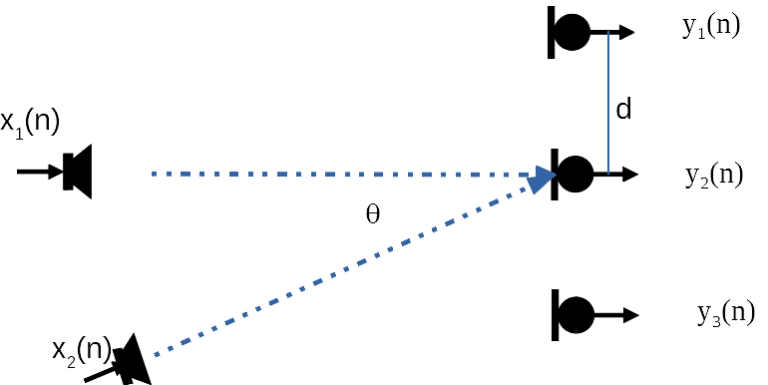
Generalizing Figure 1 to N sources to M microphones, we have the microphone captured sound vector,

$y_m\left(t\right)=\sum_{n=1}^{N}{s_n\ \left(t\right)e^{-j2\pi f\left(m-1\right)dsin\left(\theta_n\right)/v}}+noise_m\left(t\right)$

$=\sum_{n=1}^{N}{s_n\left(t\right)a_m\left(\theta_n\right)}+noise_m\left(t\right)$

We can further write this into the following matrix form,

$Y=AS+N$

where $Y = [y1(t), y2(t), \dots , yM(t)]$ , $S = [s1(t), s2(t), \dots , sN(t)]$ , and

$A=\left[a_1\left(\theta_1\right),a_2\left(\theta_2\right),\dots,a_M\left(\theta_N\right)\right]$ .

The covariance matrix, $R_y=E\left[YY^H\right]=AR_sA^H+R_n$ , is Hermitian and positive definite since $R_n$ is always positive definite.
By eigenvalue decomposition, $vi$ and $\lambda i$ are the eigenvector and corresponding eigenvalue, we have

$R_yv_i=\lambda_iv_i.$

The noise dimension has smaller eigenvalue, which is the noise floor, while the dimensions that contain signals will have larger eigenvalue. Therefore, the noise subspace can be constructed by

$E_N=\left[v_{N+1},v_{N+1},\dots,v_M\right]$ .

The signal dimension will have smaller value if it is projected into the noise subspace. Therefore, the following formula will have larger value and appear to be a peak,

$\frac{1}{\left|E_n^Ha\left(\theta\right)\right|^2}\ =\ \frac{1}{a^H\left(\theta\right)E_nE_n^Ha\left(\theta\right)}$

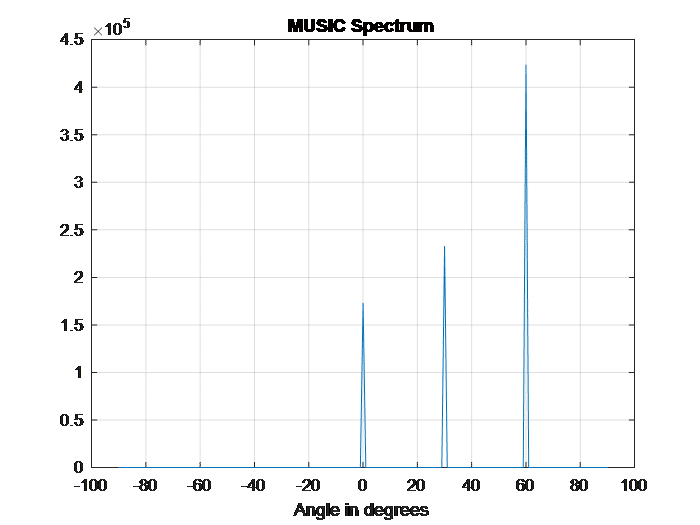
The above formula defines the MUSIC algorithm. The number of peaks indicates the number of independent sound sources and the corresponding direction $\theta$ defines the incoming direction of each sound source.
Figure 1 shows results of MUSIC algorithm for a linear array of 8 microphones. The three incoming signals impinge on the array at 0, 30, and 60 degrees from the broadside.

Complete Communications Engineering

MUSIC (Multiple Signal Classification) Algorithm