Minimum Variance Distortionless Response(MVDR) Beamforming

Minimum Variance Distortionless Response(MVDR) beamforming is a technique widely used in multi-channel acoustic signal processing. It is general enough to form a common framework to design beamforming algorithms for various physical configurations.

We assume that there are M sources that create a sound field as below. There are N microphones of a microphone array in the sound field. As shown in the figure below.

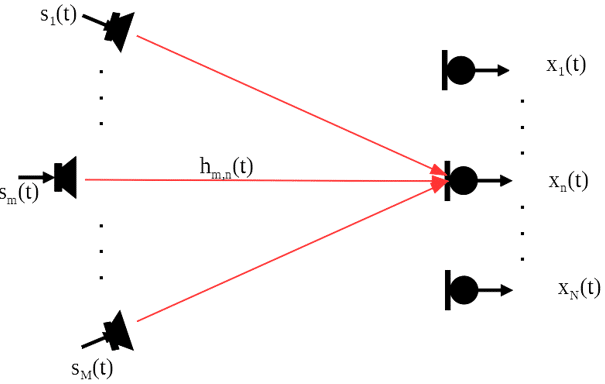
The captured sound for the n’th microphone

$x_n\left(t\right)=\sum_{m=1}^{M}{h_{m,n}\ast s_m\left(t\right)}$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\sum_{m=1}^{M}\sum_{l=0}^{L-1}{h_{m,n}\left(l\right)s_m\left(t-l\right)}.$

If our target is s₁(n), we can lump all other sound sources together into one interference term,

$x_n\left(t\right)=h_{1,n}\ast s_1\left(t\right)\ +\ \sum_{m=2}^{M}{h_{m,n}\ast s_m\left(t\right)}.$

Vectorizing the microphone captures, we have,

${{y}}\left(t\right)={{x}}\left(t\right)\ +\ {{v}}(t)$

where

$v_m\left(t\right)\ =\ \ \ \sum_{m=2}^{M}{h_{m,n}\ast s_m\left(t\right)}.$

We assume that we can separate ${{x}}\left(t\right)\$ into two orthogonal components,

${{x}}\left(t\right)={x}_{1}{x}_{I}+{x}_{Q}\left(t\right)$

where I and Q denotes the in-phase and quadrature components of ${{x}}\left(t\right)\$ with respect to ${x}_{1}$ .

${x}_{I}=\frac{E\left[x_1\left(n\right)x\left(n\right)\right]}{{E}\left[{x}{1}^{2}\right]}$

and

${x}_{Q}\left(t\right)\ ={{x}}\left(t\right)\ -\ {x}_{1}{x}_{I}$ .

By the orthogonality principle, we can derive the MVDR solution,

$h_{{MVDR}}=\frac{E\left[y_1\left(n\right)y\left(n\right)\right]^{-1}E\left[x_Is_1\right]}{E\left[x_Is_1\right]^H\left[y_1\left(n\right)y\left(n\right)\right]^{-1}E\left[x_Is_1\right]}$

Complete Communications Engineering

Minimum Variance Distortionless Response(MVDR) Beamforming