Full Plane Least Squares Acoustic Sound Source Localization

The need to pinpoint the exact originating point of acoustic sources is gaining traction for applications such as gaming and conferencing. While there are a number of solutions that are readily available for half-plane source localization of point sources, the existing literature that can be leveraged for full plane point source location estimation is limited. This is partly due to the complicated topology of the microphone array required to distinguish one half plane from the other. We present an approach using the minimum number of microphones required to realistically be able to have a birds-eye view of an entire plane. We also do not make the assumption that the source is from a far field and as such, our approach can be utilized for both far field and near field models and further produce a closed form solution devoid of simulated annealing like searches.
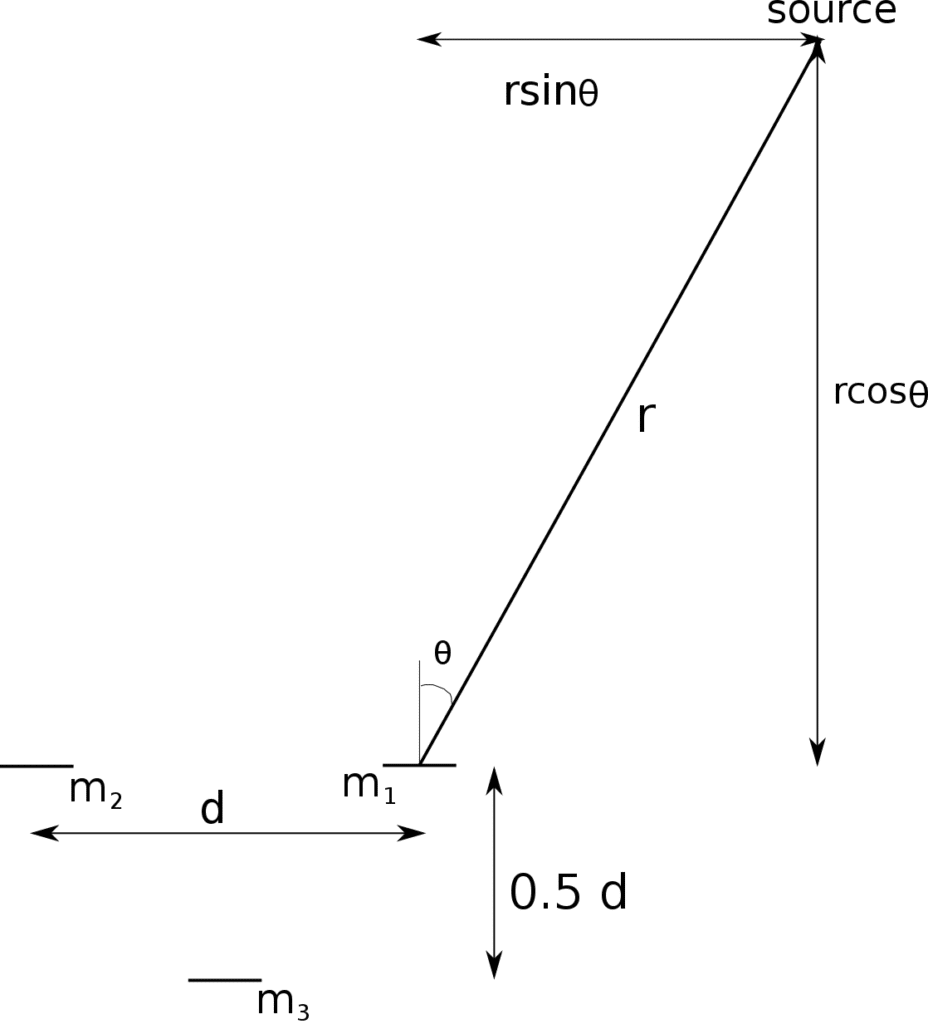
Consider an acoustic signal impinging $3$ microphones, subtended at an angle of $\theta^{\circ}$ on one microphone. The signal at microphone $i$ , $x_i$ , can be denoted as

$x_i(t) = s(t - \tau_i) + \nu_i(t), i \in \{1, 2, 3\}$

where $\tau_i$ is the delay of the desired signal at microphone $i$ from the source, $s(t)$ is the source signal, $\nu_i(t)$ is noise and $c$ is the speed of acoustic signals. Both $s(t)$ and $\nu (t)$ are zero mean ergodic processes. We will like to estimate the angle of arrival and range from $s(t)$ anchored on a specified microphone. The setup is as shown in Figure 1.

Figure 1: 3 microphones

The pair-wise time difference of arrival, $\tau_{i,j} = \tau_j - \tau_i$ can be obtained using GCC-PHAT, coherence, or any optimal algorithm for a particular application. Note that, even though these approaches, GCC-PHAT etc, are used primarily for angle of arrival estimations, their primary intermediate output is the time difference of arrival at paired sensors before data fusion to determine angle of arrival. The range of the source from each sensor, $1$ to $3$ , as depicted on Figure 1 is given as:

$r_1 =r$
$r_2 = \sqrt{\left(d + r\sin{\theta}\right)^2 +(r\cos{\theta})^2}$
and
$r_3 = \sqrt{\left(\frac{1}{2}d + r\sin{\theta}\right)^2 +\left(\frac{1}{2}d + r\cos{\theta}\right)^2}$

It can easily be shown that the equations above can further be reduced to achieve

$c^2 d \left( \tau_{1,2}^2 - 2 \tau_{1,3}^2\right) \sin{\theta} +d\left( c^2\tau_{1,2}^2 -d^2\right)\cos{\theta} = cd^2 \left(\tau_{1,2} - 2 \tau_{1,3}\right) + 2c^3 \tau_{1,2}\tau_{1,3} \left( \tau_{1,2}-\tau_{1,3}\right)$

From the synthesized equation above, a $360^{\circ}$ direction of arrival is computed using least squares.

VOCAL Technologies offers custom designed direction of arrival estimation solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!

Complete Communications Engineering

Full plane least squares acoustic sound source localization

More Information