Fast, efficient and finite set SRP-PHAT angle of arrival estimation for beamforming. Estimation of the angle of arrival (AoA) of acoustic signals is essential in acoustic beamforming. There are therefore various research on high resolution algorithms for estimation of AoA. One such algorithm is steered response power with phase transform, SRP-PHAT, which is touted because of its robustness in reverberant environments. The drawback for SRP-PHAT algorithm is the computational cost for the grid-search component, which is akin to simulated annealing. We present a go-around to this problem of computational burden by noting that our interest lies in the AoA and not the location of the originating source. To be precise, the AoA estimation problem is as follows:
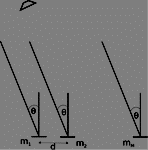
Consider a far field acoustic signal impinging a uniform linear array (ULA) of microphones with separation distance
at an angle of
. The signal at microphone
,
, can be denoted as
where is the channel impulse response,
denotes convolution,
is the delay at microphone
,
is the source signal and
is a zero mean ergodic process. The setup is as shown in Figure 1.
ULA of microphones with pairwise distance of
Conventionally, SRP-PHAT makes use of frequency domain computation. However, it is easy to show that using the physical constraints on the separation distances of the microphones, for each pair of microphones, computations will suffice as opposed to
using the fast Fourier transforms approach, where
and
is the maximum sample delay between the two microphones,
and
. Thus, we will leverage the time domain analytic equation for SRP-PHAT
where is the cross-correlation between the data from microphones
and
with
and
is an integer delay corresponding to a look angle. The main idea here is in the details of the look direction. The Sampling frequency and the microphone separations place a limit on a finite number of look angles with each look angle corresponding to a set of delays across all microphones. Suppose the maximum delay samples between the reference and microphone
is
, then the cardinality of the look directions,
) with each look direction having M-tuple delays, one for each microphone is given by
where the factor of two is for positive and negative angle of arrivals.
For example, for three microphones uniform linear array with pairwise consecutive microphone distance corresponding to delay samples, there will be
3-tuples of look directions which can be memoized if needed. The M-tuple corresponding to the angle that maximizes
is returned with the AoA given by the least squares expression
with corresponding time difference of arrivals being for the
that maximizes
.
The computational complexity for microphone ULA with frame size of
is upper bounded by
VOCAL Technologies offers custom designed AoA estimation solutions for beamforming with a robust voice activity detector. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!