Modal beamforming uses a Fourier decomposition to analyze a soundfield. Its design allows for frequency invariant beampatterns and compensation for wave interaction with the array body. Here we will focus on the circular microphone array and its relationship with cylindrical harmonic decomposition.
When dealing with circular arrays, we can take advantage of its azimuthal symmetry by utilizing the cylindrical harmonic decomposition. The expansion of the sound pressure is represented as
where is the cylindrical harmonics. Fourier coefficients P are defined as
The above equations are analogous to the Fourier analysis and synthesis equations. As with spherical harmonics, cylindrical harmonic expansion holds completeness, satisfying orthogonality and normalization. This allows for the field to be expanded using linear independent basis functions.
Let us now assume that the circular microphone array is unbaffled circular aperture in the free-field with omnidirectional sensors. The modal response is defined as
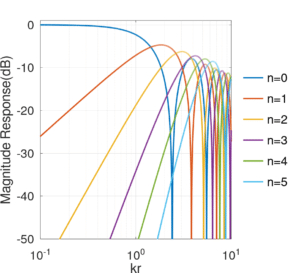
where is the Bessel function of the first kind of the nth order. The coefficients
describe the impinging plane-wave. A baffled array has similar description, giving
where is the Hankel function and ‘ denotes the first derivative. Conventional beamformers, such as delay-and-sum, do not compensate for the scattering of waves of off the array surface. By using the baffled case, scattering is described in the second term, yielding a more robust beamformer.