Noise Models in Testing of Sound Capture Signals

Microphone array sound capture consists of a desired source signal accompanied with additive noise. It is therefore advantageous to approximate noise fields during testing of a beamformer. The coherence function,

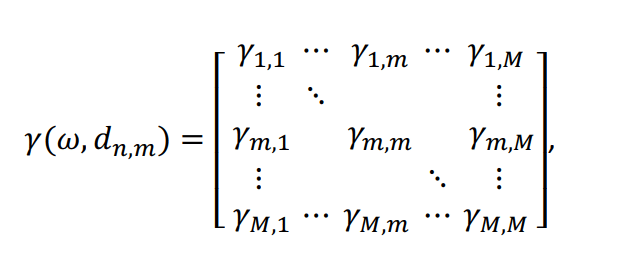
is one representation utilized to estimate the spatial correlation of noise in a microphone array of M sensors. Here, we will discuss two noise field estimations: spherically isotropic and cylindrically isotropic. Both approximations assume the noise field is an infinite sum of uncorrelated plane waves. We also assume omnidirectional elements in the microphone array.

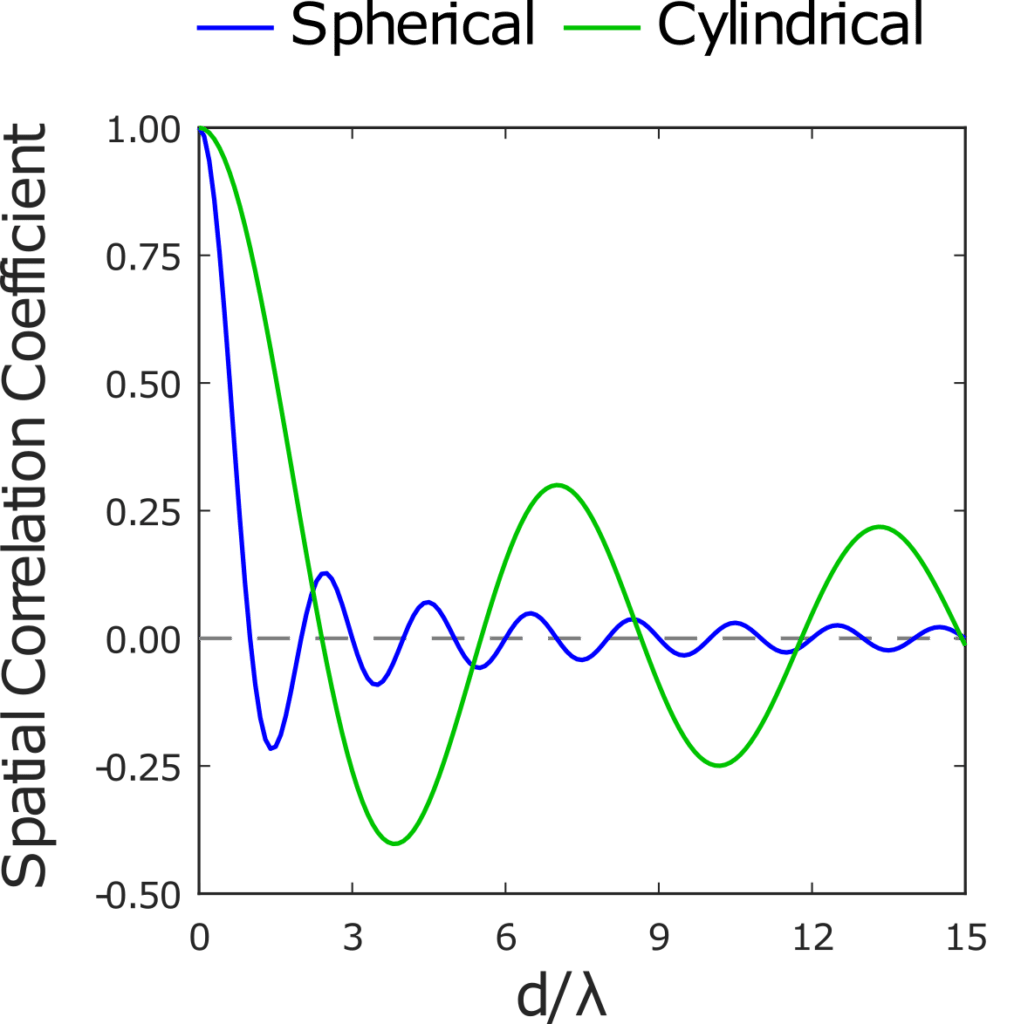
Figure 1. Comparison of spherical and cylindrical spatial correlation
coefficients as a function of inter-sensor spacing over wavelength.

Consider the spatial coherence function of a plane wave,

$\gamma_{n,m}(\omega)=\frac{1}{A}\oint\text{e}^{-\text{j}kd_{n,m}\cos\phi}d\text{A},$

where $k$ is the wavenumber, $\omega$ is the incidence angle of the plane wave, and $dn.m$ is the distance between the nth and mth sensor. For a spherically isotropic field, the coherence function can be calculated using the unit surface area of a sphere, giving

$\gamma_{n,m}(\omega)=\frac{1}{4\pi r^2}\int_{0}^{2\pi}\int_{0}^{\pi}\text{e}^{-\text{j}kd_{n,m}\cos\phi}r^2 \sin(\phi)\,d\phi d\theta$

Applying u-substitution, $u=kd_(n,m) cos(\theta)$ , the spherically isotropic coherence function is

$\gamma_{n,m}(\omega) = \frac{1}{2kd_{n,m}}\int_{-kd_{n,m}}^{+kd_{n,m}} \text{e}^{-\text{j}u} d\text{u}$
$\gamma_{n,m}(\omega) = \frac{\sin(kd_{n,m})}{kd_{n,m}}$
$\gamma_{n,m}(\omega) = \text{sinc}(kd_{n,m})$

The spherically isotropic coherence function best serves as a model for a three-dimensional diffuse field, where noise is travelling in all directions with equal power. The same computation utilizing the unit surface area of a cylinder yields

$\gamma_{n,m}(\omega)=\text{J}<em>0(kd</em>{n,m}),$

where J is the zero-order Bessel function of the first kind. The cylindrically isotropic noise field, or two-dimensional diffuse field, models noise within a room with an absorptive ceiling and floor causing the soundfield to propagates longitudinally within the enclosed space. As seen in Figure 1, correlation between two sensors decreases at a higher rate in a spherically isotropic field. This results in a higher directivity index (gain) in the three-dimensional diffuse field.

Complete Communications Engineering