Head-Related Transfer Functions | VOCAL Technologies

A head-related transfer function (HRTF) describes the interaction between a propagating wave and a listener’s head, ears, and torso. The transfer function is defined for each ear, giving

$H_{\phi,\theta} (\phi,\theta,r,\omega) = \frac{G_{\phi,\theta}(\phi,\theta,r,\omega)}{F(\phi,\theta,r,\omega)},$

where $\phi$ is the azimuth angle, $\theta$ is the elevation angle, $r$ is the distance, and $\omega$ is the specified angular frequency. $G_{\phi,\theta}(\phi,\theta,r,\omega)$ represents the transfer functions from the source to the subject’s auditory canal while $F(\phi,\theta,r,\omega)$ is the reference measurement from the source to the center position of the head without the subject. Deconvolving . $G_{\phi,\theta}$ equalizes the signal, removing the source and microphone responses, giving the HRTF.
The HRTF is a very individualized measurement due to the vast variations of the human body, ear, and head shape. The measurement process is a time-intensive procedure. With sensors placed in the subject’s ears, the source rotates around the subject, taking measurements at a given resolution. This has led to a major push in faster measurement techniques, such as the reciprocal HRTF measurement technique.

Figure 1. Example of binaural head-related impulse response and head-related transfer function. (Top) Head-related impulse responses (HRIR). (Bottom) Head-related transfer functions. (Kemar MIT Media Lab HRTF Database)

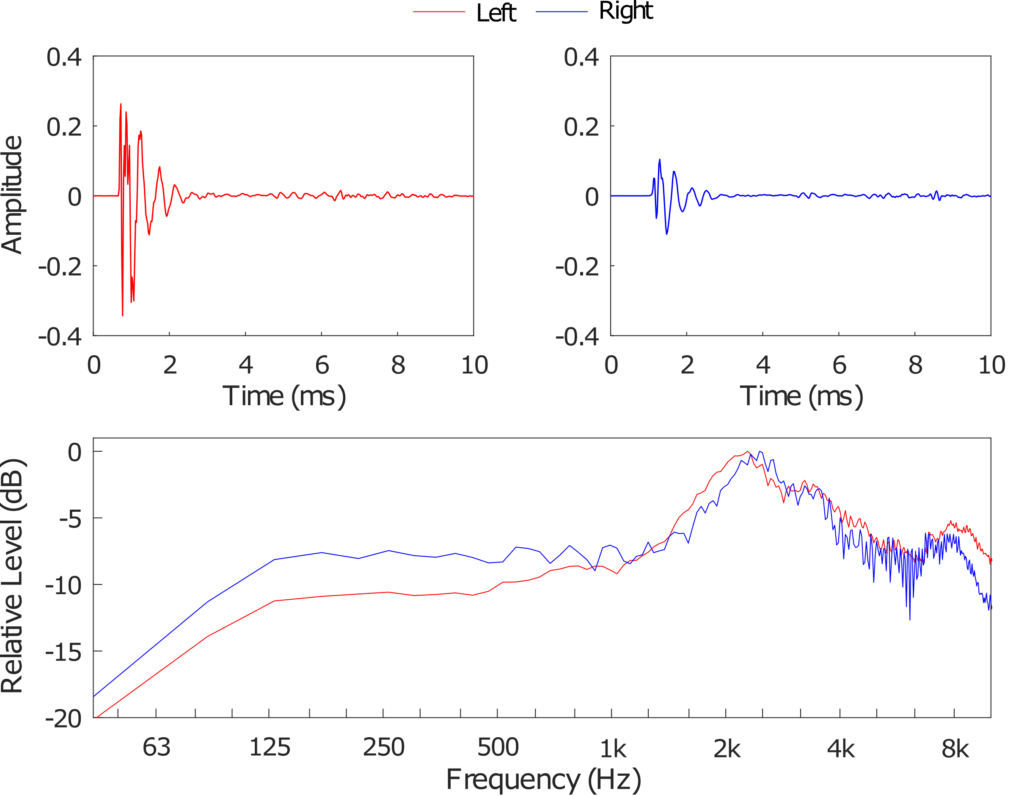
The HRTF is essential in spatial audio application of binaural rendering. Not only does a non-individualized HRTF degrade the ability to localize a virtual source, but it also distorts perceived externalization, where the source is perceived outside of the listener’s head. Research has also focused on numerical modeling and the interpolation of sparse datasets neural networks.

Complete Communications Engineering