Knowledge enhanced compressive sampling array

According to the compressive sensing theory, the success of compress sensing depends on two essential principles: sparsity and incoherence. The sparsity implies that the signal can be compressively sensed, which is based on the fact that many natural signals are sparse or compressible in an appropriate basis. The incoherence between the compressive sensing basis and the signal representation basis guarantees the reconstruction of the sparse signals from compressive measurements. Now, it is well known that random compressive sensing matrices, such as Gaussian matrix and Bernoulli matrix, exhibit a very low coherence with any fixed representation.

Although it is robust, unfortunately, random sensing basis does not exploit any other knowledge of the signals besides the sparsity. In practical applications, e.g., 5G cellular network, some users’ information is available from the previously observed data or from the tracking information of current users. With such a priori knowledge, the compressive sensing matrix can be optimized for better reconstruction performance.

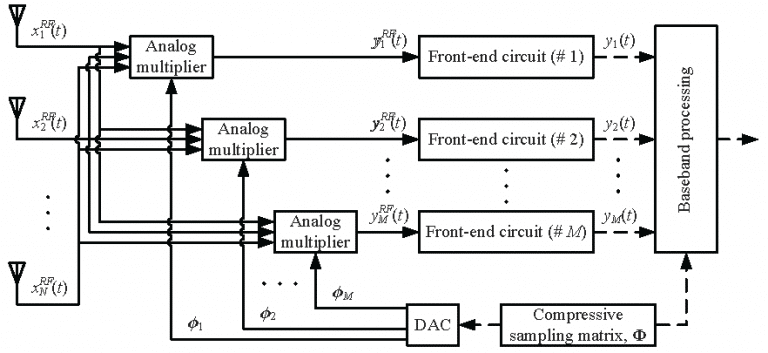
Considering the direction-of-arrival (DOA) estimation using compressive sampling array, as shown in Fig. 1, the compressive sensing matrix can be optimized by minimizing the minimum mean-square error (MMSE) of the parameter estimation as

$\min_{\boldsymbol{\Phi}} E \{ \| \boldsymbol{\theta} - \hat{\boldsymbol{\theta}} \|_{2}^{2} \} \nonumber$

or maximizing the mutual information between the compressive measurements and the parameter to be estimated as

$\max_{\boldsymbol{\Phi}} I(\boldsymbol{y}; \boldsymbol{\theta}). \nonumber$

Here, $E\{\cdot\}$ and $I(;)$ denote the statistical expectation and the mutual information, respectively. Both the objective functions are the implicit function of the compressive sensing matrix $\boldsymbol{\Phi}$ . Due to the relationship between mutual information and minimum mean-square error, the sensing matrix $\boldsymbol{\Phi}$ obtained from either optimization problems is the optimal one.

Simulation

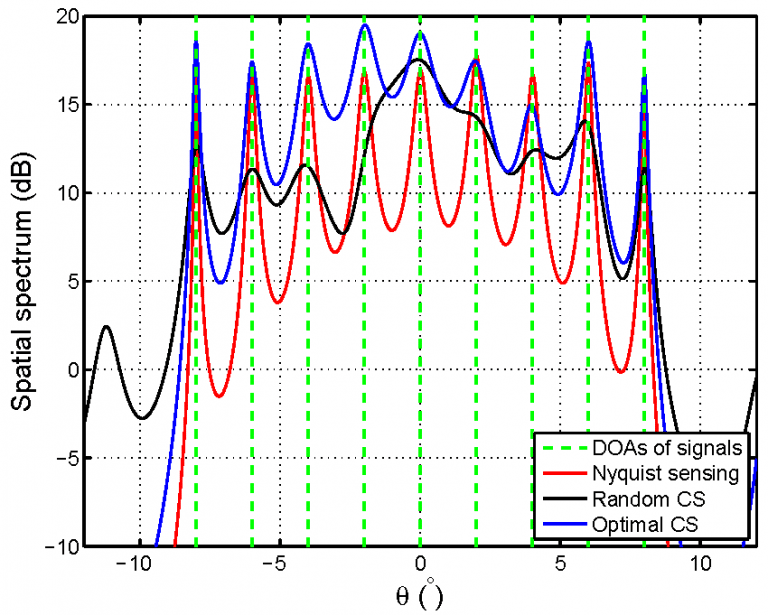
Assume a uniform linear array with 50 omnidirectional sensors equipped at the base station in a massive MIMO system. After 5 times compression, the dimension of the compressed measurement vector $\boldsymbol{y}(t)$ is reduced from 50 to 10. Fig. 2 compares the Capon spatial spectra of different compressive sampling schemes. Evidently, by exploiting the a priori knowledge of the users, the optimized compressive sampling can clearly identify the nine users as the Nyquist sampling, while the random compressive sampling does not provide sufficient resolution to identify all nine users.

Product Offerings

VOCAL Technologies offers custom designed, knowledge enhanced compressive sampling solutions in 5G systems. Our custom implementations of such systems are meant to deliver optimum performance for your compressive sampling tasks. Contact us today to discuss your solution!

Complete Communications Engineering

Knowledge enhanced compressive sampling array