DOFs enhancement using sparse array

Direction-of-arrival (DOA) estimation is one fundamental application in array processing, which has been widely used for various fields including radar, speech, wireless communications. Limited by the Nyquist sampling rate, uniform arrays, such as uniform linear array (ULA) and uniform circular array, are the most popular ones. The main disadvantage of uniform arrays is that the number of estimated sources should not be larger than the number of array sensors, i.e., the so-called degree-of-freedom (DOF) constraint.

Sparse arrays, e.g., coprime array and nested array, can be used to increase the DOFs, such that the number of estimated sources can be larger than the number of array sensors. Hence, it is appealing for DOF enhancement.

Fig. 1. Illustration of array configurations. (a) The coprime array. (b) The interpolated ULA.

As Fig. 1 demonstrates, the interpolated ULA can be implemented by interpolating additional sensors in the sparse array where the physical sensors do not exist. According to the low-rank property of the interpolated ULA covariance matrix, the covariance matrix of the interpolated ULA can be recovered by solving the following rank minimization problem

$\begin{array}{rcl}&\min\limits_{\boldsymbol{z}}& \mbox{rank}(\mathcal{T}(\boldsymbol{z})) \nonumber \\&\mbox{subject to}& \left\vert \mathcal{T}(\boldsymbol{z}) -\hat{\boldsymbol{R}}_{\boldsymbol{y}_{\mathrm{U}}\boldsymbol{y}_{\mathrm{U}}} \circ \boldsymbol{B} \right\vert_{F}^{2} \le \delta \nonumber \\&& \mathcal{T}(\boldsymbol{z}) \succeq \boldsymbol{0}, \nonumber \end{array}$

where $\mathcal{T}(\boldsymbol{z}) \succeq \boldsymbol{0}$ denotes a Hermitian positive semidefinite Toeplitz matrix with $\boldsymbol{z}$ as its first column, $\boldsymbol{B}$ is a binary matrix distinguishing the known (non-zero) elements and the unknown (zero) elements in the initialized sample covariance matrix of the interpolated ULA $\hat{\boldsymbol{R}}_{\boldsymbol{y}_{\mathrm{U}} \boldsymbol{y}_{\mathrm{U}}} = \frac{1}{K} \sum_{k=1}^{K} \boldsymbol{y}_{\mathrm{U}}(k) \boldsymbol{y}_{\mathrm{U}}^{\mathrm{H}}(k)$ with $K$ snapshots, $\mbox{rank}(\cdot)$ denotes the rank of a matrix, $\| \cdot \|_{F}$ denotes the Frobenius norm, and $\delta > 0$ is a user-defined parameter to constrain the covariance matrix fitting error. The above non-convex rank minimization problem can be efficiently solved by introducing the nuclear norm convex relaxation.

Simulation results

In the simulations, we deployed a coprime array with coprime integers 3 and 5. Namely, the physical coprime array and the interpolated ULA has 7 and 13 sensors, respectively. Fig. 2 shows the DOF improvement using sparse array, namely, using 7 physical sensors can estimate up to 12 sources.

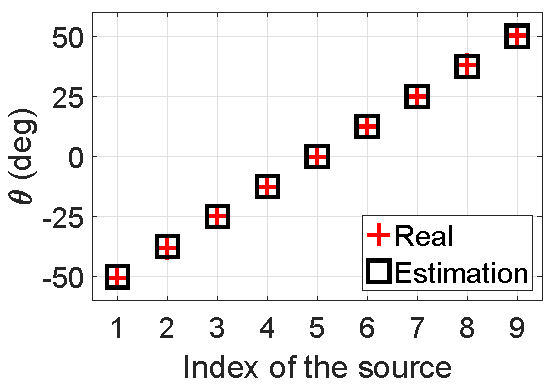
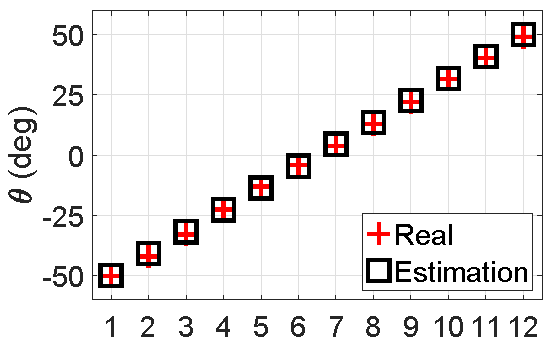
Fig. 2. DOFs illustration of the proposed DOA estimation algorithm. (a) 9 sources; (b) 12 sources.

Product Offerings

VOCAL Technologies offers custom designed DOA estimation solutions with increased DOFs. Our custom implementations of such systems are meant to deliver optimum performance for your specific DOA estimation task. Contact us today to discuss your solution!

Complete Communications Engineering

DOFs enhancement using sparse array