Howling detection based on LMS algorithm

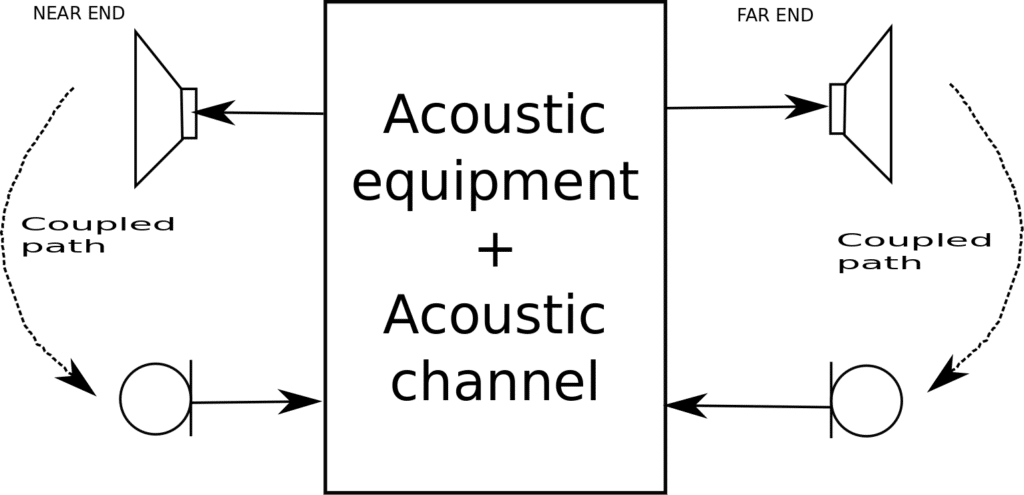
Howling is a closed loop oscillatory feedback usually due to a high volume loudspeaker signal. This arises due to a coupling path that exists between the loudspeaker and the microphone both at the near end and far end rooms. The phenomenon is illustrated in Figure 1 below:

Figure 1: Howling generating acoustic coupling path

Howling consists of an oscillatory signal with either speech or noise. Thus, the far end and near end microphones will be picking the same signal with a measure of attenuation and phase shifting. The frequency of the howling sinusoidal is however the same. Consider a howling sinusoidal at the loudspeaker of the near end room, denoted

$s(t)$ , as: $s(t) = A \cos{(\omega t + \phi_o)}$

Now suppose the near end microphone picks up a noisy and sampled signal

$x[n] = \sum\limits_{k = 0}^{L-1} h[k] s[n-k] + \nu[n]$

The a short time spectrum can be synthesized as:

$x(\omega) =A_n \pi \left(\delta(\omega - \omega_o) + \delta(\omega + \omega_o) \right) e^{j\omega \phi_n} \sum\limits_{k = 0}^{L-1} h[k] e^{-j\omega k}$

The task now is to estimate $\omega_o$. A $\frac{\pi}{2}$ phase shifted version is easily synthesized by Hilbert transformation to attain another signal

$x_p(\omega) = -j A_n \pi \left(\delta(\omega - \omega_o) - \delta(\omega + \omega_o) \right) e^{j\omega \phi_n}\sum\limits_{k = 0}^{L-1} h[k] e^{-j\omega k}$

An adaptive filter output will be given as:

$y(w) = w_1(\omega) x(\omega) + w_2(\omega) x_p(\omega)$

The error signal is then given as:

$e(w)= s(\omega) - y(\omega)$

A choice of the update filters as:

$w_1(\omega) = \frac{A}{A_n \sum\limits_{k = 0}^{L-1} h[k] e^{-j\omega k}} \cos{(\phi_n -\phi_o)}$

and

$w_2(\omega) = -\frac{A}{A_n \sum\limits_{k = 0}^{L-1} h[k] e^{-j\omega k}} \sin{(\phi_n -\phi_o)}$

will drive the error to zero.

VOCAL Technologies offers custom designed solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!

More Information

Complete Communications Engineering