Hadamard Transform Digital watermarking is based on a the Fast Hadamard Transform that offers fast processing time and reduced complexity. The technique is robust against a majority of attacks and has a good transparency property.
The Hadamard transform is an orthogonal transform that decomposes a signal into a set of orthogonal, rectangular Hadamard (or Walsh) functions. This transform is performed only in the real domain and the basis functions have only values ±1, therefore this transform does not require multiplications.
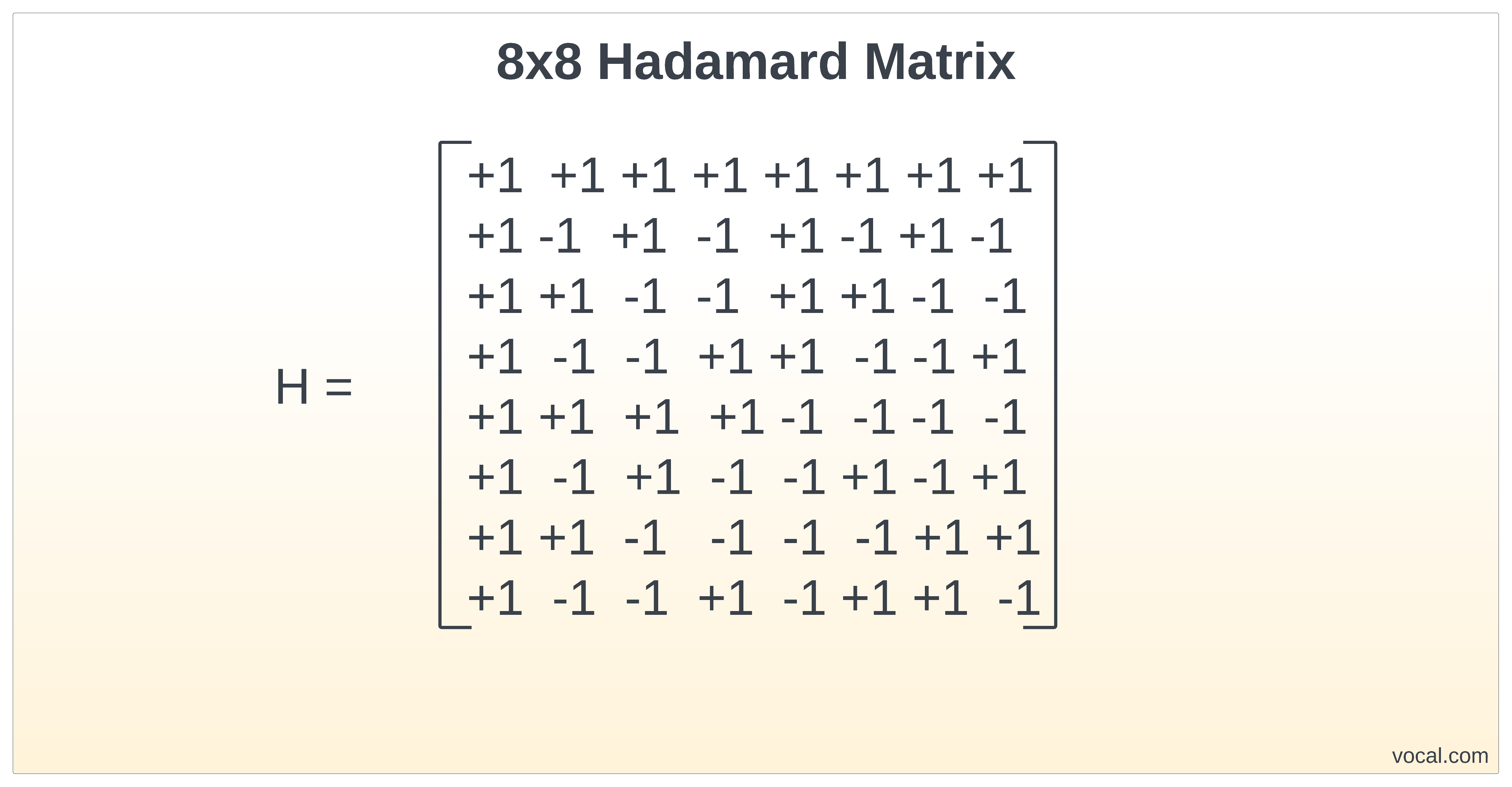
The Hadamard matrix is a square matrix of ±1 values. Its rows are orthogonal to each other and its columns are orthogonal to each other. The product of a Hadamard matrix to its transpose is the identity matrix scaled by N.
The 2-D Hadamard direct transform can be represented as:
where
- Ic – represents the input 2-D signal,
- Iw – the output 2-D signal and
- H – is a Hadamard matrix with size NxN, where N is a power of 2
The 2-D Hadamard inverse transform can be represented as:
The Hadamard Transform Digital Watermarking is usually applied in the luma domain of the source (cover) image. The cover image is divided into 8×8 blocks denoted as Ic(n), where n is the number of the block. For each block, the entropy value E(n) is determined. Select blocks where the entropy value is greater than some particular threshold and determine the Hadamard Transform for those blocks. Split the digital watermark image into the set of 8×8 blocks.
Assuming that the watermark image is a binary image, multiply each 8×8 watermark block by a constant value λ and add to the Hadamard Transforms of the selected blocks in the 8×8 cover image. For each of the selected blocks determine the inverse Hadamard transforms. To create the watermarked image, insert inverse Hadamard transformed blocks into the original cover image.
The watermark extraction algorithm is similar to the insertion algorithm. For the selected blocks of the watermarked image, the Hadamard Transform has to be applied. From transformed blocks, watermarks may be extracted by subtracting transforms of the selected blocks of the original cover image.
More Information
VOCAL’s solution is available for the above platforms. Please contact us for specific supported platforms.
