The Bessel and Henkel functions are special functions in mathematics. This function expresses inward or outward propagating waveforms, such as a circular membrane or line source. Moreover, the function also has a unique form describing the radial dependence of a spherical waveform. We will focus on an overview of the Bessel and Hankel functions.
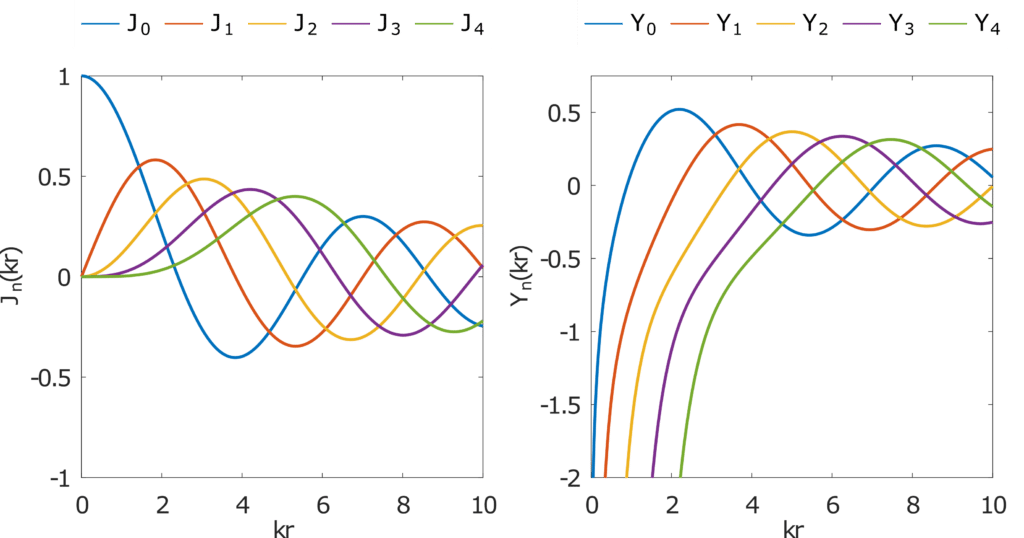
The cylindrical form of the Helmholtz equation is given by
where k is the wavenumber. Applying separation of variables, we assume . Substituting and dividing by P yields
The third addend is only dependent on z, meaning it must be a constant. This gives
.
Defining the radial wavenumber as and multiplying by
yields
Observing that the second term is independent of r and z, we assume this term is also equal to a constant,
After substitution, the expression is an ordinary differential equation dependent on r,
The above differential equation is the Bessel equation. The general solution is given as
where is the Bessel function of the first kind of order n and
is Bessel function of the second kind of order n. The Hankel functions are two linearly independent combination of the Bessel function:
The Bessel functions may also describe the propagating wave in a spherical sense. These functions are called spherical Bessel functions j. The relationship between Bessel and spherical Bessel functions is given as
where the order n is a half-integer, n+1/2, instead of an integer.