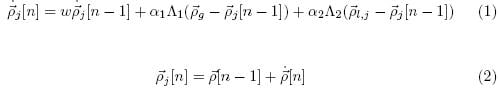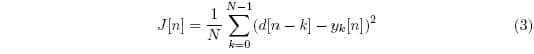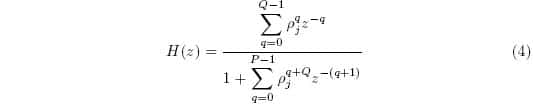Particle Swarm Optimization (PSO) is an optimization algorithm used in Acoustic Echo Cancellation. PSO, originally developed in [1], was inspired by group dynamics of social behavior and is a hybrid of evolutionary search and neural network training algorithms.
Particle Swarm Optimization
For each particle, the algorithm is written as:
Where →pj is the jth particle’s N-dimensional position vector, ∙→p is the velocity vector, →pg is the best position found by any particle in the swarm, pl,j is a vector containing the best N-dimensional position the jth particle has found, w is the inertial weight, α1 is the group acceleration constant, α2is the individual acceleration constant, and Λi = diag[λ1, λ2, …, λN]i where λji ϵ U[0, 1].
PSO in Adaptive IIR Filtering
PSO can be used to adaptively converge IIR filters. Using the MSE as our criterion for convergence, the cost function to minimize using PSO becomes:
Where d is the desired signal, i.e. the far end speech put through the echo path, and yk,j is the estimate, i.e. the far end speech convolved with the echo path model, given by the jth particle. The adaptive IIR filter will have the following structure:
With paj being the qth dimension of the jth particle, with Q+P = N where Q is the number of zeros and P is the number of poles. Then the signal estimate becomes:
Where x denotes the far end speech. As [2] explains, there are variety of adaptations to the basic algorithm that need to be made for adaptive IIR filtering. For instance, the authors explain that in order to ensure convergence, the random numbers must be different across matrices, the positions of some of the particles must include additive random noise to help escape from local minima different from the global minimum, and both must be controlled logically in order to ensure a covering of the space. In addition, stability can be improved by converting the adaptive filter structure into a parallel form of second order filters, and have each filter search within a region called the stability triangle.
Real Time Implementation of PSO
Modified PSO
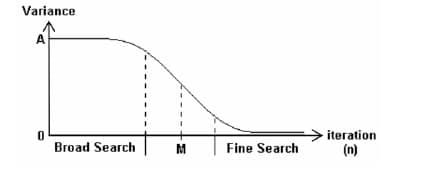
The Modified PSO algorithm was originally developed in [3] for use in an adaptive filtering environment. Essentially, it is adaptive because the particles positions and parameters are periodically randomized, ensuring the algorithm does not stagnate at local minima and can adapt to a changing error surface. The variance of this randomization is scheduled to decrease with time according to a sigmoid:
Where A is a constant, M is the iteration of the sigmoid’s midpoint, and S is the sigmoidal slope. Thus, initially the randomization variance is high, leading to the particles being forced to search globally. As time goes on, the algorithm is presumed to be converging on the global optimum, and thus the variance is decreased. This schedule is illustrated in the following figure:
Figure 1: Randomization Variance Schedule [3]
Amongst the things to be randomized are the particles positions around the global optimum. This allows the region to be searched thoroughly from every direction. Secondly, the variance of the distribution for the λ’s is scheduled as above in order to ensure a finer search around the global optimum. Local minimum can be avoided by selecting at random a subset of particle positions to be randomized, thus ensuring escape for at least some particles. Lastly, since the region around the global optimum will inevitably be searched most thoroughly, the authors randomized according to a distribution that sparsely populated the surrounding region. In this way, redundant searching can be greatly reduced.
Adaptive PSO
The Adaptive PSO algorithm [4] is intended for adaptive use. It is a fuzzy state space algorithm that utilizes adaptive control of the PSO parameters according to likelihood of the current state. To build the metric for state membership, we first define:
Where ζj is the mean Euclidean distance of the swarm from the jth particle, N is the number of particles, and D is the dimension of solution space. Then letting ζg denote the metric from the best particle, we can define the closest particle as ζmin and the farther particle as ζmax in an evolution factor f defined as:
Where f ϵ R[0,1] The membership of the swarm to a particular state depends fuzzily on this metric. For an exact description of the state breakdown, please see [4]. This evolution factor is then used to control the inertial weight as:
Where w ϵ R[0.4,4.9]. This dependence on f is essentially a dependence on the current state, and thus will benefit the swarm’s searching capability. In addition, the acceleration coefficients αk are varied according to the following heuristic scheme:
Figure 2: Acceleration Coefficient State Space Scheme [4]
The Speed Up Factor
Despite PSO being an already quickly converging optimization routine, there is a trick given in [5] that can help speed up its convergence. The idea is to break the swarm overlapping groups and block process the algorithm at a faster rate. For each group, the position update equation now becomes:
Where m is the speed up factor. Now the particles will be moving much faster, so to compensate yet still keep the same resolution, we increase the sampling frequency. By doing the computation in parallel yet overlapping blocks, we can simulate a great many particles cheaply. This essentially solves the convergence vs complexity problem, as we are greatly reducing the computational complexity while still increasing the real time convergence rate. The exact value of m is system specific and thus will be determined by the designer.
For more information about determining optimal coefficients:
Design of Adaptive IIR filters
References
[1] J. Kennedy, R. Eberhart, “Particle Swarm Optimization”, Proceedings I.E.E.E. International Conference on Neural Networks,Washington DC, vol. 4, pp. 1942-1948, 1995.
[2] D.J.Krusienski, W.K.Jenkins, “Particle Swarm Optimization for Adaptive IIR Filter Structures”, Congress on Evolutionary Computation, vol. 1, pp. 965-970, 2004.
[3] D.J.Krusienski, W.K.Jenkins, “Adaptive Filtering via Particle Swarm Optimization”, Conference Record of the Thirty-Seventh Asilomar Conference on Signals, Systems, and Computers, vol. 1, pp.571-575, November 2003.
[4] Z. Zhan et al, “Adaptive Particle Swarm Optimization”, IEEE Transactions on Systems, Man, and Cybernetics – Part B: Cybernetics, vol. 39, no. 6, pp. 1362-1380, December 2009.
[5] W. Liu et al. “Real-time particle swam optimization based current harmonic cancellation”, Engineering Applications of Arti_cial Intelligence, vol. 24, pp. 132-142, 2011