It may seem that spectrum subtraction noise reduction is only based on an engineering intuition. However, this engineering intuition has a direct mathematics connection to the theoretically optimal Winer filter approach. The basic spectrum subtraction in frequency domain,
(1)
if N(f) is available or can be estimated.
We can write is as the following,
(2)
![\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{\left|X\left(f\right)\right|^2-\left|N\left(f\right)\right|^2}{\left|X\left(f\right)\right|^2}\left|X\left(f\right)\right|^2\](https://s0.wp.com/latex.php?latex=%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%5C+%3D%5Cfrac%7B%5Cleft%7CX%5Cleft%28f%5Cright%29%5Cright%7C%5E2-%5Cleft%7CN%5Cleft%28f%5Cright%29%5Cright%7C%5E2%7D%7B%5Cleft%7CX%5Cleft%28f%5Cright%29%5Cright%7C%5E2%7D%5Cleft%7CX%5Cleft%28f%5Cright%29%5Cright%7C%5E2%5C+&bg=ffffff&fg=000000&s=0 "\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{\left|X\left(f\right)\right|^2-\left|N\left(f\right)\right|^2}{\left|X\left(f\right)\right|^2}\left|X\left(f\right)\right|^2\")
(3)
and we can recognize immediately the spectrum subtraction approach is actually equivalent to the Wiener filtering solution. Therefore, spectrum subtraction is mathematically optimum in the same sense as Wiener filtering!
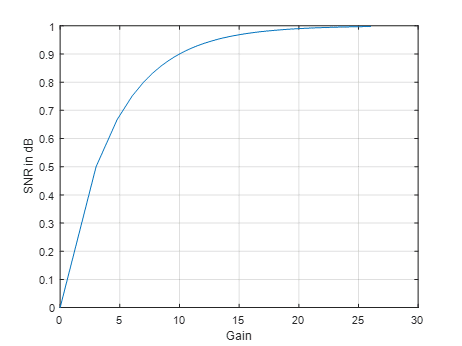
The spectrum subtraction approach can be viewed as zero phase filter with frequency response
and 0< H(f) < 1. It applies a SNR-dependent gain to the noisy signal. When the SNR is high, the gain applied is high while SNR is low, the gain is low.
The main conceptual difference between Wiener filtering and spectrum subtraction is the in way the gain factor is represented. In spectrum subtraction, the powers are estimated locally in time, or we may say, instantaneous power, while Wiener uses statistical ensemble.