This note is an extension of the note ON SYNTHETIC NOISES FOR VOICE ENHANCEMENT, [1]. It is a common task to generate random noise of a predefined spectrum. While there are several efficient methods of generating such a noise signal, in this note we limit ourselves to briefly describing three of them.
The first method is based on the inverse Fourier transform. A practical guide is provided in [2], Annex C. The principle there is to use Inverse Discrete Fourier Transform, IDFT, (or Inverse Fast Fourier Transform, IFFT) with predefined amplitudes, according to the given specification of the predefined spectrum. The randomization of the generate signal is achieved by means of using random number generation when computing the phases of individual spectral components of the IDTF.
Specific steps are as follows:
- based on the predefined power spectrum density, generate complex amplitudes (using square root function for the absolute amplitude values);
- generate random phases that are to be associated with respective absolute amplitude values; use random number generator producing uniform distribution of phase values spread over the segment [0, 2π];
- compute IDFT (or IFFT) using the complex amplitudes defined earlier;
- using DFT (of FFT) verify that the random noise Power Spectral Density (PSD) corresponds to the predefined target.
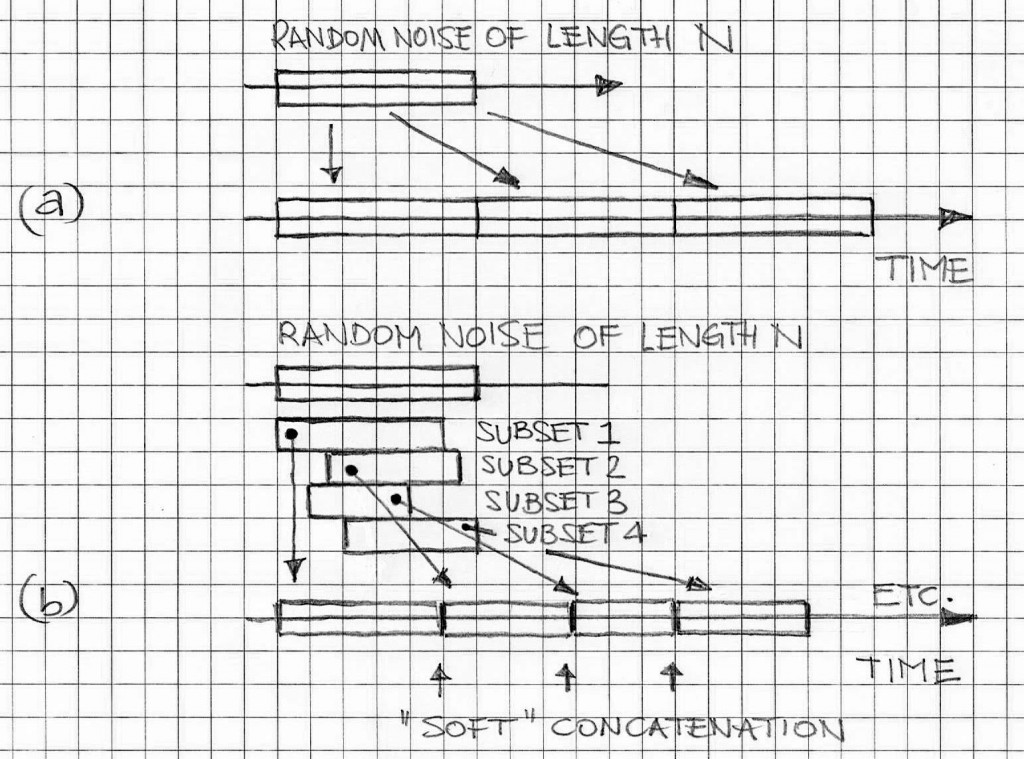
There is one significant caveat related to this method of generating random noise with a predefined spectrum. The length of the noise train is equal to the size N of the DFT. Suppose that Fs is 16kHz and N = 214; then time duration of the noise is approx. 1 second. Very often that is not adequate for most practical applications. Therefore, there are two options to consider. The first option is to increase the size of DFT. The second option is to generate non-periodic extensions of the segment of length N. The second option is computationally less costly but it slightly affects the PSD. Figure 1 illustrates the concept of non-periodic extensions.
The second method designs frequency sampling-based digital FIR filters with arbitrarily shaped frequency response. Once the FIR filter’s coefficients are determined, the white noise is used as an input to the FIR filters while the output is the random noise of the desired PSD. An extension of that approach is described in detail in [3]. The core of the extension presented there is a Forward Least Squares (FLS) algorithm to the design of FIR filters. The study [3] also elaborates on the FIR2 method (FIR2 is a MATLAB library function used for designing frequency sampling-based digital FIR filters with arbitrarily shaped frequency response) and compares these two approaches.
The third method is based on Yule-Walker algorithm (cf. [4, 5]). The Yule-Walker algorithm recursively, using the least-squares (LS) criterion, finds the Mth order IIR filter whose magnitude frequency response matches the predefined random noise spectrum. Similar to the second method (as well as its extension), in order to obtain the random noise of predefined spectrum, one needs to apply the white noise signal to the input of the designed filter and the output of the filter is the approximation (in the LS sense) of the desired random noise.
The topic of synthetic random noise generation of the predefined spectrum, analysis and usage consist of many fine technical details. Contact us to discuss these and other details with VOCAL engineering staff.
More Information
References
- ON SYNTHETIC NOISE FOR VOICE ENHANCEMENT
- ITU-T, G.168-2012 (02/12); Digital Network Echo Cancellers
- Finite Impulse Response Filter Design Using A Forward Orthogonal Least Squares Algorithm, Wu, X., et el, White Rose Research, University of Sheffield, 2005.
- Introduction to Time Series Analysis, Peter Bartlett , Stanford University, 2010.
- The Yule Walker Equations for the AR Coefficients, Gidon Eshel, University of South Carolina