There are several synthetic random noise signals used in Voice Enhancement. The most popular, by any measure, is white noise. White noise is casually defined as a random signal with energy uniformly distributed across all frequencies. So, its name appears to suggest that the term white noise originated from white light. In digital representation, the white noise spectrum extends from 0Hz to the Nyquist frequency (i.e., to Fs/2) and has constant power spectral density (PSD).
This definition does not preclude the signal’s probability density function (PDF). Typically, the white noise generators produce signals of Gaussian PDF. Other PDF’s of practically used random noises include uniformly flat PDF. It is interesting to observe that only trained listeners can distinguish audibly machine generated pseudo-white noises of different PDF. The human hearing is much more sensitive to frequency contents than to statistical distribution of random signal local values.
While the white noise concept and its models are very useful from the viewpoint of modeling and simulating system behaviors, the white noise is an idealization of random signals and, strictly speaking, it does not exist in real life. Much better representations of real-life random signals are “colored” noises (that is, random or pseudo-random signal whose PSDs are not constant across the entire frequency band).
There are several popular non-white, i.e., colored random noise types in use in audio/acoustic/DSP practice. Pink noise is defined as random noise whose the power spectral density. S(f) is given by the following formula
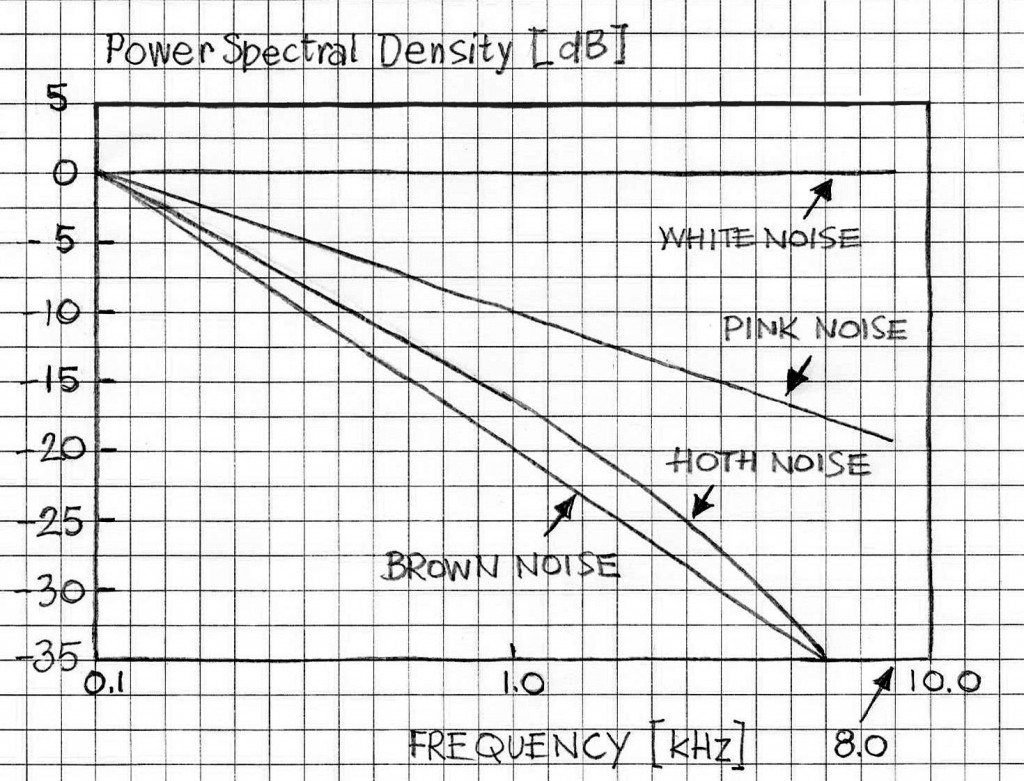
It is worth underscoring that unlike more general definitions, this one is specific in terms of the spectral density: the pink noise’s power spectral density decays with frequency at the rate of 3 dB per octave.
Example 1: Let’s take frequency f=f1=440 Hz (tone A4 concert pith), and compare to f=f2=2*f1 (i.e., the tone which is one octave higher than f1). Then, the descent of PSD in one octave is as follows:
where pink_drop_per_octave quantity indicates the rate of power spectral density decay with frequency normalized to one octave.
A more general definition of pink noise is sometimes quoted in technical literature (cf. [3]): the pink noise is referred to as any random noise signal whose PSD S(f) satisfies the following:
where α satisfies the following
In fact this is not a very common definition. Some prefer to call any random noise whose power spectral density satisfies (2) with the constraining formula as per (3) as pinkish noise, which is definitely a broader definition.
Many sources, including software audio tool manuals, refer to the random noise whose spectrum density S(f) satisfies the following formula:
as brown noise (which originally came from Brownian motion-inspired noise; thus the term does not come from the color but after Robert Brown, the discover of Brownian motion).
As Equation 4 indicates, the brown noise’s spectrum decays at the rate of 6dB per octave. This rate of descent of PSD is reflected in subjective audible perception; the brown noise sounds softer and warmer.
Hoth noise that was created to reflect the background noise which is present in a typical office environment. Although the original paper on this type of noise was written long time ago, in 1941, the signal is still being used in audio and DSP practice (cf. ITU-T P.800) (cf.[1-5]).
Hoth noise’s PSD S(f) starts @ ~5 dB/octave and ends (@ 8kHz) with a slope of ~26dB/octave. It definitely sounds softer and warmer than the pink noise. At the same time is sounds a bit less warm than the brown noise, despite the fact that its S(f) is below the brown noise’s S(f) for frequencies approaching the Nyquist frequency. Subjectively speaking, the Hoth noise is a good alternative to “pinkish” noise and it is often used as a comfort noise in Voice Enhancement applications.
Figure 1 shows PSD curves of common synthetic noises using in audio and DSP and, specially, Voice Enhancement applications. The graphs are plotted in double logarithmic scales for Fs of 16000 Hz.
In addition to the synthetics noises mentioned so far there a concept of gray noise: a random noise subjected to a psychoacoustic equal loudness curve (such as an inverted A-weighting curve) over a given range of frequencies, giving the listener the perception that it is equally loud at all frequencies. The gray noise is not a common noise signal used audio/acoustic/DSP practice.
Sometimes there is a requirement to generate random noise of pre-determined PSD. In such a case there are two basic options:
- filter the white noise using an FIR or FIR shaping filter whose amplitude characteristic is adequately approximating the predefined PSD of the desired noise;
- generate random noise by using the Fourier series representation with predefined spectral lines approximating the given PDF (cf. [6]).
The topic of synthetic random noise generation, analysis and usage extends over many technical details. Some of them are to be covered in other notes and posted at VOCAL site. Contact us to discuss your application with our engineering staff.
More Information
REFERENCES
- Room noise spectra at subscribers’ telephone locations, by Hoth, D.F., J.A.S.A., Volume 12, pp. 99-504, April 1941.
- Sound Capture and Processing, by Ivan Tashev, A John Wiley and Sons, LTD., Publishing 2009
- Defeating Ambient Noise: Practical Approaches for Noise Reduction and Suppression Ivan Tashev, Microsoft Research, May 14th, 2006 ICASSP 2006, Toulouse, France
- OPTICOM GmbH: Fundamentals of the PSQM Measurement Algorithm
- ITU-T, P.800 (08/96); METHODS FOR SUBJECTIVE DETERMINATION OF TRANSMISSION QUALITY
- ITU-T, G.168-2015 (04/15); Digital Network Echo Cancellers.