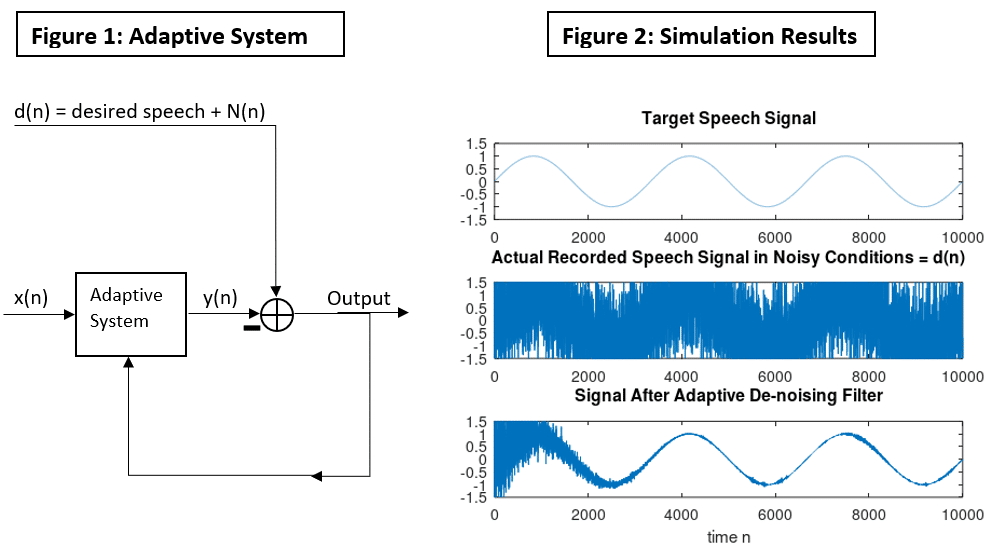
Noise Cancellation Application | VOCAL Technologies

Noise cancellation is often implemented in DSP applications using the least mean squared algorithm. A speech signal contaminated with noise may be filtered by adaptively adjusting the filter coefficients so that the output y(n) of the adaptive system is an approximation of the noise which contaminates the reference signal. As time progresses, the LMS algorithm converges to a solution which extracts the original desired signal. The premise of this application is that the input X(n) to the adaptive system must be correlated with the noise N(n) within the reference signal. That is, if a correlated model of the noise N(n) is available, the adaptive noise cancellation filter (Figure 1) can be applied to the reference signal to remove the noise by using the correlated model X(n) as an input to the adaptive system.

Recall the basic iterative procedure of the LMS algorithm:

$\mathbf{H}_{k+1}(n) = \mathbf{H}_{k} + \mu*(\mathbf{r}_{dx} - \mathbf{R}(n)\mathbf{H}_{k}(n))$ (1)

Where $r_{dx }$ and R(n) are as follows:

$\mathbf{r}_{dx}(n) = E[d(n)\mathbf{X}(n)]$
$\mathbf{R}(n) = E[\mathbf{X}(n)\mathbf{X}^{T}(n)]$

The input matrix $\mathbf{X}(n)$ is noise which is correlated with noise N(n) which contaminates the reference signal (see Figure 1). The reference signal is simply the desired signal with additive noise N(n). By computing $\mathbf{r}_{dx}(n)$ and $\mathbf{R}(n)$ , the coefficients $\mathbf{H}(n)$ may be adjusted on each iteration until the cost function is minimized via gradient descent. The resulting signal is the noise-filtered output.

Complete Communications Engineering