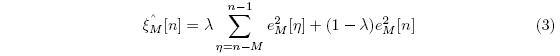To solve the problem of determining the optimal filter length for acoustic echo cancellation (AEC), the most popular method is the fractional tap length algorithm [2]. The fractional tap length algorithm is a hybrid of the earlier segmented filter algorithm and the gradient descent filter length algorithm. Since its inception, there have been many incarnations of this algorithm. The basic idea of fractional tap length algorithms is to define a fractional accumulator based on an estimate of the converged mean-squared-error and then update the optimal tap-length once it has reached a certain value.
The Filter Length Problem
The Filter Length Problem is simply how best to manage the conflicting requirements of fast convergence and full acoustic echo cancellation. This arises due to characteristics of the room impulse response. The room impulse response, also called the echo path, is typically time varying and can be broken up into the various epochs shown in Figure 1.
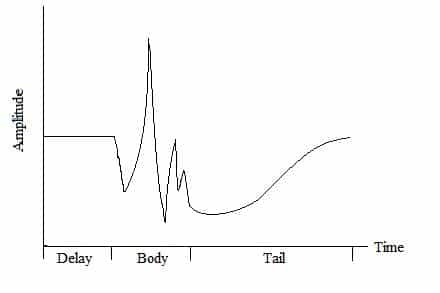Figure 1: Characteristics of the Room Impulse Response
The finite speed of sound causes a delay of the room impulse response relative to the far-end speech emission. The near end microphone then picks up a large disturbance from the impulse response’s direct coupling to the far end speech, which is followed by attenuated and shifted versions of that same response. After some time, the power in these later echoes begins to become severely attenuated, and the room impulse response relaxes in its tail.
As Figure 1 attempts to illustrate, the body of the response contains most of the information but is relatively short compared to its tail. From an engineering perspective, this allows us to model just the body with simple FIR filters, and regard the tail as an additive component of the near-end disturbance [1]. Indeed, adaptive algorithms built for FIR filters are generally simpler than those IIR filters necessitate, and require less computational resources. The problem then arises of how long to make the FIR filter. The time varying nature of an echo requires fast convergence, which implies the use of short tap lengths, but achieving full cancellation means creating a long enough filter to capture the entirety of the impulse body. In light of these conflicting requirements, we turn to structural adaptation to help determine the optimal tap length algorithmically.
The Fractional Tap Length Algorithm
Taking from the segmented filter approach, we first define a tap line of optimal length N and define a segmented error at discrete time index n with M ≠ N coefficients:
Where hM[n] is the actual value of the room impulse response at time n, w→M is the adaptive filter’s weight vector, and x→M is the far-end speech signal, starting from time n – M + 1. Taking the expected value, we obtain the segmented steady-state mean-squared-error:
This is an expected value, and thus any real time application will not have access to this information. Thus we need to have an iterative approximation, defined using an exponential smoothing factor λ as:
Which is unbiased as:
Now we let the tap-length be a time varying function and denote the change in tap length Δ. With α and β as positive constants, we arrive at the fractional tap-length accumulator:
Where sgn[·] is the signum function. α is the leak term, chosen to ensure the tap length does not grow without bound, and β is the update step-size. Finally, we quantify the tap-length update decision:
Where ⌠▪⌡denotes rounding to the nearest integer. Please refer to [2] for a more detailed version of the derivation and an implementable algorithm, and to [3] for a discussion on its steady-state performance and a useful guide to choosing the parameters.
Processing Structures for Structural Adaptation
Now that we have a robust structural adaptation method, we need to have some processing structures for an actual acoustic echo cancellation implementation. The structures discussed are the segmented structure and the backup structure.
In general, a segmented structure simply divides the impulse response into segments, and processes each with a separate filter either serially or in parallel. When a structural change in the echo path occurs, there will be transients generated from the perspective of the microphone. One method to deal with these fast changes is to place a short fixed tap-length filter in front of a longer variable tap length filter. A shorter filter will be able to deal with these types of signals better than a longer filter because it will converge faster but still be able capture most of the energy due to the transient being short-lived. After the filter, either the error output can be fed into the second longer variable tap-length filter, or into a smoothed version of the transient. Alternatively, this transient processing can be done in parallel, and the result can be used to adjust the coefficients of the longer filter before output to the far-end.
Due to the finite nature of an FIR filter, you will always have mean-square-error in excess of the minimum-mean-square-error. In the body of the echo, this excess is proportional to the change in the n-dimensional volume of the far-end autocorrelation matrix’s associated map due to the change in its spanning set, which can be easily approximated as the trace of said matrix. The error resulting from the tail of the echo is simply due to it being essentially un-modeled due to its length. Therefore for better convergence, you might segment the response into a minimum length FIR filter for the body and an IIR filter for the tail, thus modeling it precisely.
The backup structure employs some type of memory to either speed up convergence or correct for divergence in the event of a changing microphone output. If you are confident your acoustic echo cancellation system will be used mainly in one environment or within a small set of environments, you might use a variable tap-length filter to determine the optimal filter length and coefficient profile for that environment and store it for later use. When the system is next used, this saved profile can be used as an initial value and be further adapted for the specifics of the current situation. If your coefficients start to diverge, but your state machine can give no answers as to why, this backup can serve as a refresher to correct the divergence until the state machine can determine the cause. In this way you are avoiding introducing artificial errors.
References
[1] C. Shuldt et al, “Adaptive filter length selection for acoustic echo cancellation” Signal Processing, vol. 89, 2009, pp.1185-1194
[2] Y. Gong, C.F.N. Cowan, “Structure adaptation of linear MMSE adaptive filters”‘ IEEE Proceedings of Vicsual and Image Signal Processing vol. 151, no. 4, August 2004, pp. 271-277
[3] Y. Zhang et al, “Steady-State Performance Analysis of a Variable Tap- Length LMS Algorithm”, IEEE Transactions on Signal Processing, vol. 56, no. 2, February 2008, pp. 839-845.