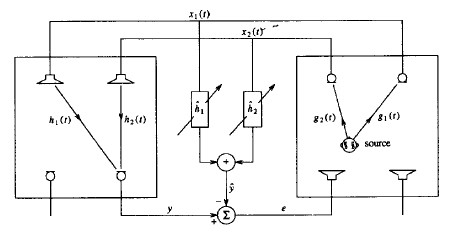
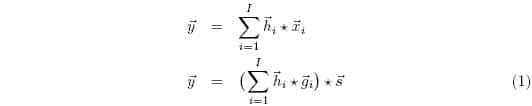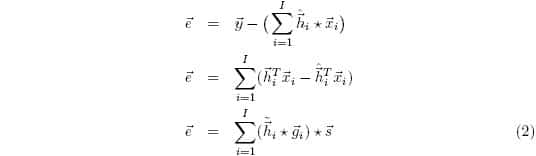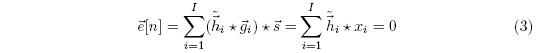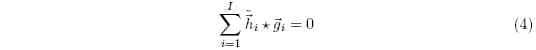The fundamental problem in stereophonic acoustic echo cancellation (AEC) is that the signals on each microphone-loudspeaker line are all correlated with each other. This implies that even when the error signal is nearly zero we might not have an accurate representation of the echo path. An accurate alignment at all times is crucial for the adaptive filter to accurately model the echo path, thereby performing optimally. Consider the problem in Figure 1:
Figure 1: The Stereophonic Problem [1]
As the figure suggests, stereophonic acoustic echo cancellation is not a simple generalization of the monochannel problem. Instead, stereophonic systems have to deal with the introduction of a second echo path they must model. Consider that you are in the recieving room on the left in the figure, and the far-end talker is in the transmission room on the right.
The talker emits a signal, denoted as 
when sampled, which becomes correlated with the echo paths between ths speaker and the microphones in the transmission room 
forming the microphone-loudspeaker line signal 
. Assuming you are being quiet, your jth microphone then picks up a signal:
Where the subscript j is dropped for simplicity, as each microphone will experience a unique echo path between the ith loudspeaker, and so the problem can be treated on a per microphone basis. The error is then written as:
Where the hat denotes an approximation, and 
. Thus when the error is zero we get:
Regardless of the talker’s signal, this leads us to the requirement that:
Thus, to ensure zero error, stereophonic echo cancellation must contend with changes in the transmission room echo paths as well. In order to keep the error constantly zero, any change in the transmission room echo path must then be accompanied by a change in one or more of the receiving room echo paths with respect to the talker’s signal. In other words, the echo path with respect to the microphone-loudspeaker signal must be well aligned.
As (3) shows, the implicit assumption to assure complete alignment, aka that 
, is that the microphone-loudspeaker signals 
are uncorrelated. If there were correlated in any way, we could not say with certainty that the adaptive filter had aligned, as the correlation may be artificially altering the microphone-loudspeaker signals, leading to low error due to happenstance rather than true alignment. One way to ensure the signals are uncorrelated is to decorrelate them yourself [2].
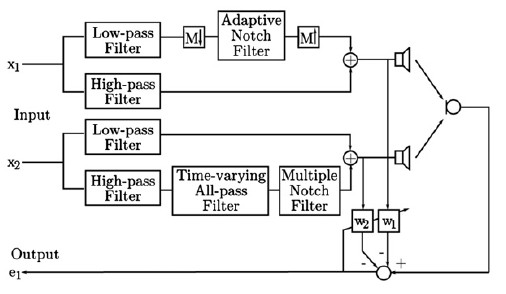
Psychoacoustic Decorrelation
Figure 2: Psychoacoustic Decorrelation Scheme [3]
One way to decorrelate the microphone-loudspeaker signal is to take advantage of the missing fundamental phenomenom, which is a psychoacoustic phenomenom where the perceived pitch stays the same despite the fact that the actual signal is missing its fundamental frequency and instead is made up of harmonics of the fundamental [3]. By using a non-stationary notch filter to remove the fundamental as in Figure 2, the signals are less correlated with respect to the mathematics, but with respect to subjective experience, not much has changed. The adaptive notch filter can be described as:
Where k0 is the parameter is used to eliminate the fundamental, and α controls the bandwidth. k0 is given by:
Where:
And thus the fundamental is estimated by:
Unfortunately, this scheme does not work for all frequencies. The missing fundamental phenomenon is a result of the majority of a signal’s energy being replaced by higher harmonics. Due to harmonic decay, the majority of this majority tends to be concentrated in the mid-range bands of the audible spectrum. Thus, the missing fundamental effect fails to work well with fundamentals above 500 Hz. Instead, [3] uses phase modulation, and [4] uses an all-pass filter to provide further decorrelation of the signals.
Variations in Cross Correlation
The real time tracking abilities of the above approach is shown in [4]. To see why the misalignment is a decreasing function of time, we consider that at each sampled time n, the cross correlation between the microphone is changing due to the changing estimate of the fundamental frequency and the time varying all-pass filter. As [2] points out, it is the variations in the cross correlation that inch the estimate towards alignment. Consider the following figure:
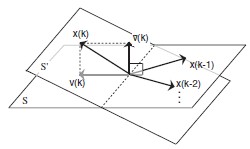
Figure 3: Subspace Interpretation of Cross-Correlation Variation [2]
In this figure, the microphone-loudspeaker signal 
where k is now the discrete time index, spans a subspace S. When the cross-correlation is constant, each new 
where m ϵ N stays completely contained in S. When the current signal 
varies with respect to the past signal, it spans new subspace S’
S. Thus, we can decompose the signal as 
with 
ϵ S and 
ϵ S’, so that represents the variation. If the coefficient updater 
, then the update is achieved with no redundancy and in the direction of convergence. This alignment behavior can be considered by examining Figure 4:
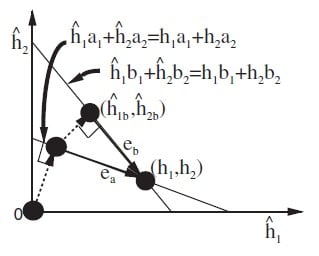
Figure 4: Geometric Interpretation of Convergence Behavior [2]
As the figure shows, if 
then varies to 
, the adaptive filter first converges to 
and then to 
. Notice then that |eb| < |ea|, and thus the error norm has decreased in the second convergence. This is because the first attempt’s solution is used as a starting point for convergence, and this first solution is closer to the true echo path than the filter was before the first attempt. Thus, varying the cross-correlation many times, the echo canceller can arrive at the true echo path.
References
[1] M.M. Sondhi, “Stereophonic acoustic echo cancellation – an overview of the fundamental problem” IEEE Signal Processing Letters, vol. 2, no. 8, August 1995
[2] S. Makino, “Stereophonic acoustic echo cancellation: An overview and recent solutions”, Acoustic Science and Technology, vol. 22, no. 5, 2001
[3] S. Cecchi et al, “A combined psychoacoustic approach for Stereo Acoustic Echo Cancellation”, IEEE Transactions on Audio, Speech, and Language Processing, vol. 19, no. 6, August 2011
[4] S. Cecchi et al, “A low-complexity implementation for a real-time decorrelation algorithm for stereophonic acoustic echo cancellation”, Signal Processing, vol. 92, April 2012