Microphone arrays measure sound waves in both time and space. The measurement data contains information about the frequency contents as well as the propagation direction and decay in space. Microphone arrays make possible the exploration of the spatial features of a sound wave.
This short section describes an interesting phenomenon, sampling aliasing, that occurs in both time domain and frequency domain. Aliasing is a fancy name for ambiguity. It means that you cannot precisely identify the true cause among several possible causes when you observe an outcome. A well known example is when we digitize an analog signal in time domain. If we sample at a slower rate than twice the highest frequency, we cannot mathematically reconstruct the original signal from the sampled signal without ambiguity. That is, we can reconstruct a sound but we have no way of telling if it is the same as the original sound.
Similarly, a microphone array has the same effect on traveling sound waves in space. In stead of describing the theory in the mathematics, we use the following simple diagram to show the concept.
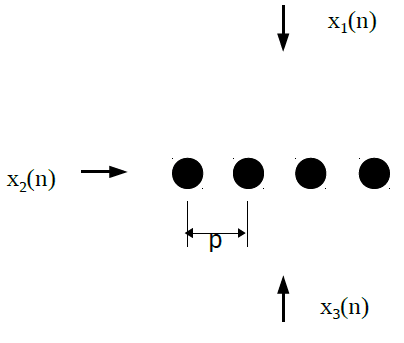
The above diagram shows a linear microphone array with 4 omni-directional microphones. The inter-mic distance is p. It is easy to see that the linear microphone array cannot tell apart a signal from the top, x1(n), and from the bottom, x3(n). However that is not the ambiguity we are interested in.
As shown in the diagram, we have a sound x1(n), impinging on the linear array from the broadside direction, and another sound source x2(n), from the left-side direction. We examine the conditions that cause ambiguity in those two directions.
If x2(n) is a monochromatic tone with wave length exactly p. Then x2 will be phased aligned at all of the microphones at all time. Regardless what signal x1(n) is, the microphone array will not be able to tell if x2(n) is present or not. Hence, there is a direction finding limitation that is related to the wavelength.
From time domain sampling theory, we know that at minimum two samples are needed to perfect reconstruct a waveform. The same applies to microphone array. Therefore, to avoid direction finding ambiguity we must have
2p < ג
or
f < v/(2p)
where v is the velocity of sound, ג is the wavelength of the sound, f is the frequency. Therefore, the maximum frequency this linear array can handle without ambiguity in direction finding is v/(2p), which is the spatial aliasing frequency.
Large separation between microphones is needed to detect low frequency contents but small distance is required to address spatial aliasing. This is the dilemma the microphone array technology is facing. At this time, state-of-the-art algorithms have only limited success in performing speech enhancement or 3D audio direction finding and reconstruction. VOCAL technologies employs microphone array technologies mainly for noise and interference reduction.