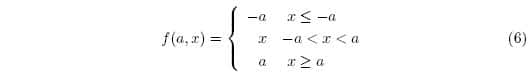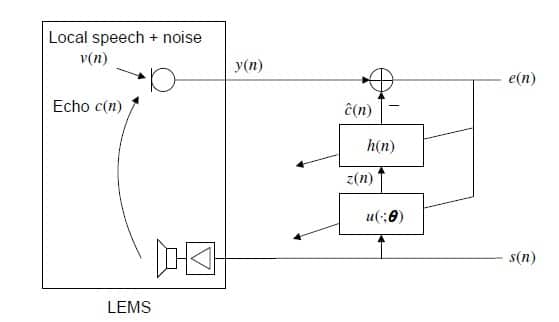
In a linear acoustic echo canceller, the non-linearity is simply modeled as a disturbing signal introduced into the microphone. Whereas in a non-linear acoustic echo canceller, the non-linearity is modeled explicitly by u(·; θ) as shown in Figure 1.
This non-linearity comes in two flavors: with memory and without.
- Memoryless non-linearity is typically a result of temperature drift in low cost hardware causing sampling rate discrepancies between the loudspeaker and the microphone, or by saturation of such systems.
- Non-linearity with memory can result from the longer time constant of electromechanical coil systems in high quality loud-speakers being longer than the sampling interval.
Hammerstein Systems
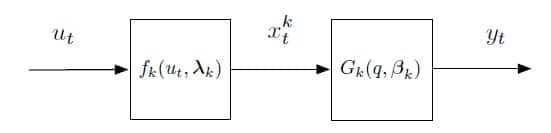
For our purposes in Acoustic Echo Cancellation, Hammerstein systems come in two major groups: Wiener-Hammerstein and Hammerstein-Wiener. Wiener-Hammerstein systems are simply a cascade of a Wiener filter in front of a Hammerstein filter. Hammerstein-Wiener systems simply reverse that ordering. Figure 2 shows an example of a Hammerstein-Wiener block used to model the echo path:
Figure 2: Hammerstein Block [2]
In this representation, 
is a non-linear map without memory that is parameterized by 
, thus making up the Hammerstein portion of the block. Then 
is a linear transfer function parameterized by 
. For acoustic echo cancellation, ut represents the far-end speech, and yt represents the estimate of the desired signal. The effective use of this type of system then depends on your ability to accurately and stably estimate the parameters. There are currently a variety of methods available.
Volterra Filters
A volterra filter of order N can be described as:
Where the hr are the rth order filter kernels, x[k] is the far-end-speech, and y[k] is the estimate of the desired signal. As you can see in (1), a high order digital realization would be impractical. Therefore, first order or second order filters are often used in combination. For instance, a second order filter in parallel with a third order filter will capture the faster convergence of the second order along with the accuracy of the third order model. Alternatively, the third order model, or even a higher order model, can be run as a shadow filter behind a lower order approximation.
Neural Networks
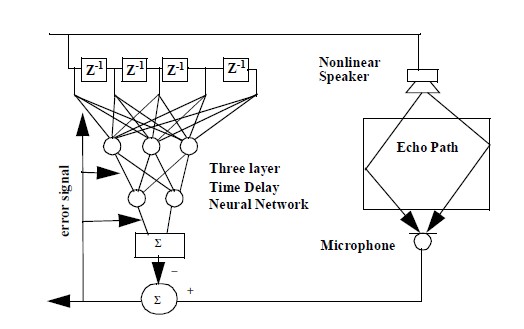
Neural Networks can be used to learn the echo path. An example is shown in Figure 3:
Figure 3: Tapped Delay Line Feed Forward Network (TDLFFN) [3]
Such a network can be trained by back-propagation. In this algorithm, we let xj be the total input to neuron j, yi be its ith output, with a weight wji:
The output of this neuron can be any function of its inputs, but originally [4], a sigmoid was used in accordance to what we see in nature. The idea is to find the wji such that a desired response is produced when given an input. To do this, we try to minimize the sum of the squared errors:
Where c denotes an input-output pair, y is the estimated signal, and d is the desired signal. To find how the weights influence the output, as to correct for the error, we find:
Then to update the weights, we use a 1-st order recursive learning rule that alters their convergence rate rather than their actual value:
Non-Linear Mappings
Non-linearity can be modeled more generally by any non-linear function placed in the parallel to the echo path. For instance, one approach is to use a hard clipper, defined as:
This equation is typically used to model saturation non-linearities in the loudpseaker or microphone, as is a sigmoid function. Alternatively, you might choose to model the loudspeaker coil as a first order differential system through its counter electromotive force. Temperature drift can be modeled with directed or bridged Brownian motion. The most general mapping can be found by fitting autoregressive integrated moving average (ARIMA) models to the residual echo that results after the FIR filter.
Processing Structures
The most pressing questions in designing a non-linear acoustic echo canceller are what non-linear model to use, and where to place that model in the echo path. Complicating things is the notion that the echo path itself may not be entirely linear. Assuming it is linear, you have the option of placing it before, after, or in place of the standard FIR adaptive filter. The placement should then keep in mind the non-linearity you are trying to capture. For instance, a model of the loudspeaker coil should be placed before the FIR fiter, but a model of microphone clipping should be placed afterwards. Neural networks offer the most flexibility when it comes to identifying non-linearity. As [3] shows, the TDLFFN illustrated in Figure 3 can be used alone or in cascade with a standard FIR filter adapted by NLMS. In addition, there are a variety of learning algorithms illustrated in the literature that can be used alone or in combination. With Neural Networks, the possibilities are almost endless.
References
[1] K. Shi, “Nonlinear Acoustic Echo Cancellation”, Ph.D., Georgia Institute of Technology, 2008.
[2] A. Wills, B. Ninness, “Estimation of Generalized Hammerstein-Wiener Systems,” presented at the 15th IAC Symposium on System Identification, Saint-Malo, France, 2009.
[3] A.N. Birkett, R.A. Goubran, “Acoustic Echo Cancellation Using NLMS-Neural Network Structures”, Proceedings I.E.E.E. International Conference on Acoustics, Speech and Signal Processing. Detroit, Vol. 5, pp. 3035-3038, 1995.
[4] D.E.Rumelhard et al, “Learning representations by back-propagating errors”, Nature, pp. 533-536, October 1986.