Non-Linear AEC

Non-linearities of the acoustic echo path limit performance of any linear echo canceller. Figure 1 demonstrates how different physical conditions limit performance of an acoustic echo canceller.

The non-linearities-related limit of ERLE is typically the second most factor affecting the ERLE. In some designs, the first one is related to the enclosure vibrations. Practically speaking though, quite efficient methods of addressing this effect are by improving the loudspeaker housing.

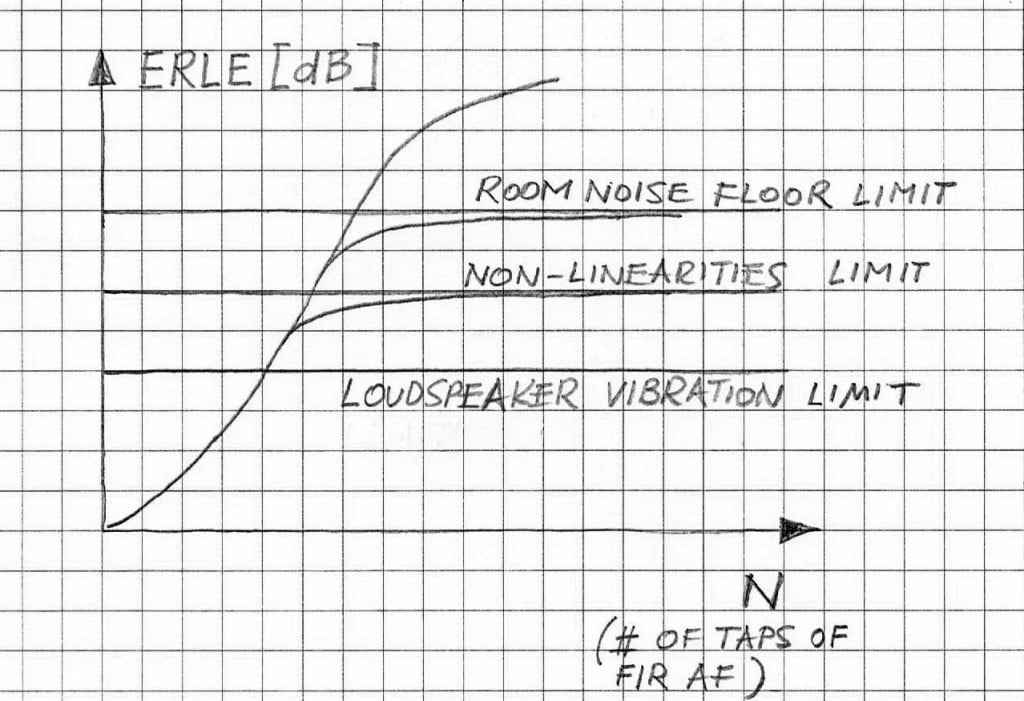
The non-linearities-related factors limiting achievable ERLE are mostly associated with typical implementations of loudspeaker design. There are several reasons for loudspeakers introducing non-linearities. Among those, the most prominent are:

• nonlinear force deflection characteristic of the loudspeaker cone suspension system;
• non-uniform magnetic field which causes that the cone displacement produced by the current flowing through the loudspeaker’s coil is not linearly related to the current.

These two effects are not the only non-linear effects observed in loudspeakers. Other include higher vibration modes of the loudspeaker’s  cone as well as other non-linearities.

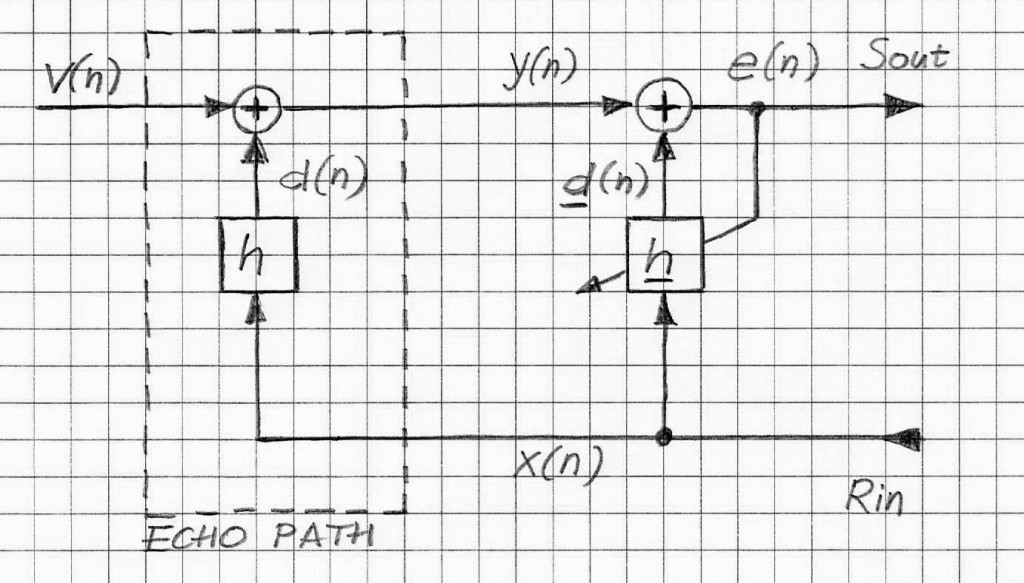
If the echo path (including loudspeaker and microphone) is linear, then the relationship between the input x (a.k.a. R_out) and output y (a.k.a., S_in) is linear. Therefore y and x are related by the following well known formula:

                                                                 (1)

where h_1,i(n) is the standard transfer function (or impulse response, or Volterra kernel of the 1^st order) of the linear time invariant system (cf. Fig.2)

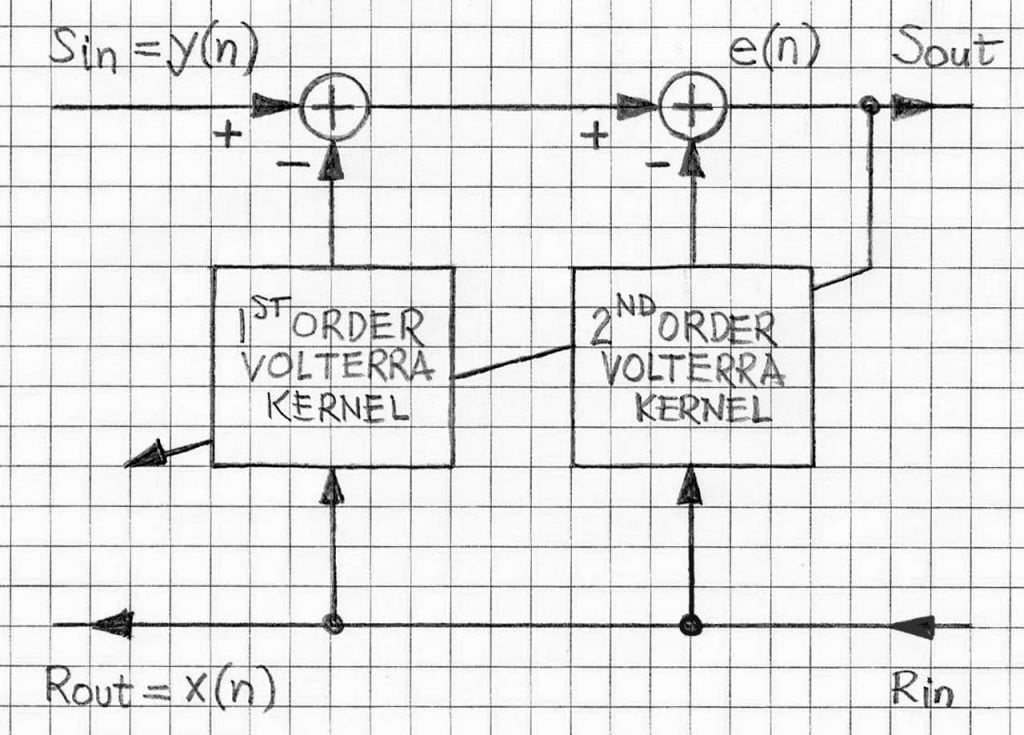
If the echo path is non-linear then the x-y relationship is given by the Volterra series that employs Kth order Volterra  kernels h_{K,i,j,…,r(n)},  i,j,…,r = 1,2,…,K.

The Kth order Volterra  series representation of y(n) (output) versus x(n) (input) is as below (cf. Refs.[2,3]):

                                                (2)

where

                                                                (3)

                                        (4)
,
,
,
     (5)

where the upper summation limit (not specifically indicated in Eqs. 3-5) is N where N corresponds to the length of the echo path coverage.

In the case applicable to AEC where the most of non-linearities are associated with the loudspeaker, the 2^nd -order Volterra series is practically quite adequate for representing the overall echo path and thus for improving ERLE in the AEC converged state; the 3rd-order Volterra series representation of the echo path is used in some very advanced AEC  realizations; in such cases numerical processing of the 3^rd-order Volterra kernel-based part takes the most of the CPU power needed for the AEC under consideration; the computational burden associated with that part is the main limitation of practical implementations of non-linear AEC (cf. Ref.[4]).

In Figure 3, a block diagram of an AEC’s adaptive filter based on the 2^nd-order Volterra series is shown. In the case of the NLMS algorithm the error and the normalized step size are straightforward extensions of the linear case. The computational complexity of the 2^nd-order part, after exploiting symmetry of the 2^nd-order Volterra kernel, is estimated as 3/2 N² + 3/2 N + 2 (as compared to 2 N + 2 for 1^st-order Volterra kernel) (cf. Ref[5]).

VOCAL’s linear Acoustic Echo Canceller design has been successfully tested in typical acoustical environments and deployed widely.  It is ported onto many of the typical DSP processors. If required, the 2^nd-order Volterra kernel part can be added to the C-based code; practical realization will require though that there is adequate CPU power that supports the non-linear version of the AEC.

REFERENCES

1. Limitations of handsfree acoustic echo cancellers due to nonlinear loudspeaker distortion and enclosure vibration effects, A. N. Birkett, R. A. Goubran, in IEEE ASSP Workshop on Appl. of Signal Processing to Audio and Acoustics, 1995; pages 103 – 106
2. The Volterra and Wiener Theories of the Nonlinear Systems, by Schetzen, M., Robert E. Krieger Publ. 1998
3. Adaptive Filters; Theory and Applications, Farhang-Boroujeny, B., John Wiley and Sons, 1999.
4. Stochastic gradient based third-order Volterra system identification by using nonlinear Wiener adaptive algorithm, Chang, S.-L. and Ogunfunmi, T.,; IEEE Proceedings – Vision Image and Signal Processing 05/2003;
5. NONLINEAR ACOUSTIC ECHO CANCELLATION WITH 2ND ORDER ADAPTIVE VOLTERRA FILTERS, Stenger, A. et al, University of Erlangen-Nurnberg, ICASSP ’99, vol.2.

More Information

• Echo Cancellation Design