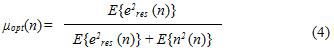In echo cancellation, proper control of step-size and regularization parameters of the normalized least mean squares (NLMS) can improve the overall performance of the system. The filter update equation for NLMS is
| (1) |
where μ(n) is the variable step-size and ε(n) is the variable regularization. The main goals of these control parameters and of any adaptive algorithm is to increase the convergence speed, minimizing the system distance and decrease the divergence rate in the presence of noise. Analysis of how these parameters affect the performance of the adaptive algorithm reveals how these parameters can be made time variable to achieve these goals, and thus greatly improve the overall performance of an echo canceller.
Adaptive filter theory shows us the relationship the step-size and regularization parameters have on the mis-adjustment, and the convergence speed of the echo cancellation system. For example, the convergence speed is
| (2) |
where Τmax, is the maximum time constant and λmin is the minimum eigenvalue of the autocorrelation matrix R. As we can observe from (2) is that convergence speed is inversely proportional to the step-size. The mis-adjustment is described as
| M = μTr(R) | (3) |
where M is the mis-adjustment and Tr(R) is the trace of the autocorrelation matrix. This shows that the mis-adjustment is proportional to the step-size. The translation of these results for the regularization parameter results in reversing the proportionality. Combining the results of (2) and (3), results in an engineering trade-off between convergence speed and the system distance. Therefore, for initial convergence or re-adaptation, the step-size should be close to one and the regularization should be close to zero, and as the mis-adjustment approaches zero, the step-size should approach zero and the regularization should approach infinity. In acoustic echo cancellation (AEC), the ability to vary the step-size (or lower the regularization value) is an important characteristic for environments in which the echo path is time-varying.
In addition to controlling the convergence speed and mis-adjustment, the step-size and regularization parameters can be used to control the influence of noise into the system. This noise includes the presence of the near-end talker and/or local background noise. As discussed in the Double-Talk Detection in Echo Cancellation, when significant levels of near-end and far-end signals are present simultaneously, adaptation needs to be frozen in order to prevent divergence. Therefore, an optimal step-size parameter should be decreased by the presence of noise. To put this result together from the results of the previous paragraph, the optimal step-size parameter should be
where
is the expectation value of the residual error power, and
is expectation value of the noise power. As one can observe, when the residual error signal is large, the step-size will be close to one, and when the presence of local noise is large, the step-size is close to zero. This scaling is important in hands-free communication systems set in environments with large levels of background noise, such as drive-thru’s and factory settings.