Impulse Response Estimation for Audio via Complementary Sequences

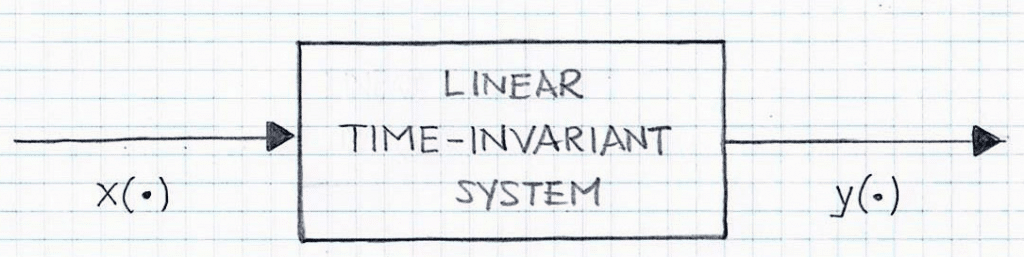
Estimation of impulse responses of audio devices and acoustic systems requires careful statistical processing of data in order to minimize adverse effects of background noise. In the case of audio and acoustics, adverse effects of background noise influencing impulse response estimation are quite significant. Therefore, techniques to minimize influence of background noise or other uncorrelated and undesired signals are of prime importance. A linear time-invariant (LTI) system whose impulse response is to be estimated using input (x) and output (y) signals is shown in Figure 1.

A straightforward technique that is used in practice is based on exciting the LTI system via a long sequence of impulses. Illustration of that approach is depicted in Figure 2. In order to get an adequate separation between the impulse response estimate and the background noise, a large number of impulses exciting the LTI are needed. In addition to that, parameter ΔT (i.e., the time distance between input pulses) has to be carefully chosen. While selecting a small value of DT allows for an increase of impulse excitation repetitions in the pre-determined time duration of the experiment (and thus resulting in greater separation of the estimated impulse response from uncorrelated background noise), application of the consecutive pulse prematurely, i.e., before response to the previous one does not die down sufficiently, will produce a systematic error. Therefore, selection of ΔT has substantial influence on the accuracy of the system impulse response estimation.

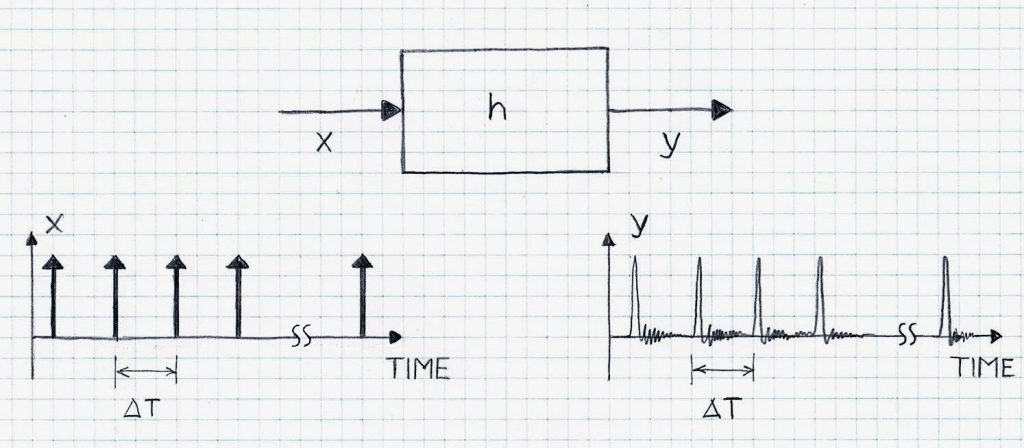
Example: Suppose the LTI System is a small office characterized by RT₆₀ of 150 milliseconds. The rule of thumb is that  ΔT > RT₆₀ . The larger ΔT is, in comparison to RT₆₀ , the more accurate estimation of the impulse response is going to be. Thus, let us assume that the chosen ΔT is equal to 3 . RT₆₀ . Hence  ΔT = 450 milliseconds. Assuming that we need to repeat application of the excitation pulses 1000 times (as that would ensure the random errors caused by the background noise and other random audio disturbances will average out adequately), the time needed for the output data collection is going to be 7.5 minutes.

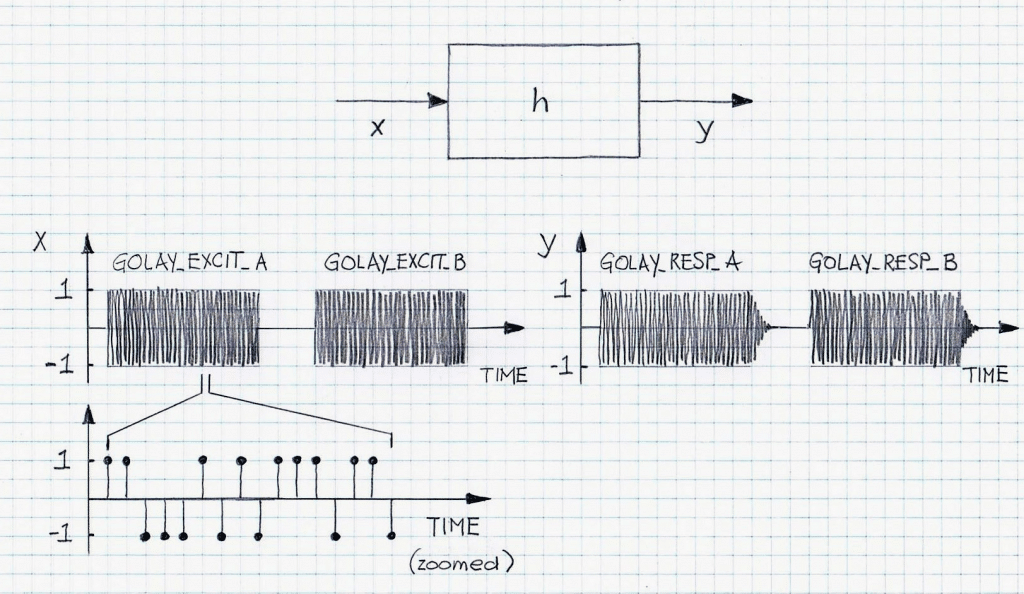
Alternate approach to estimation of LTI system impulse response is by using Golay Complementary Sequences (GCS) approach.  A pair of Golay Complementary Sequences can be generated using the following pseudo code:

% Initialization:
Golay_A = [1 , 1];
Golay_B = [1, -1];

Define N ; % N is sequence length in samples

% Sequence generation
while N > 1
Previous_Golay_A  =  Golay_A;
Previous_Golay_B  =  Golay_B;
Golay_A  =  [Previous_ Golay_A, Previous_Golay_B];
Golay_B =  [Previous_ Golay_A, -Previous_Golay_B];
N = N -1;
end

The above pseudo-code uses a property of Golay Complementary Sequences that if Golay_A and Golay_B are Golay sequences, [Golay_A, Golay_B] and [Golay_A, -Golay_B] are also Golay sequences.

Golay Complementary Sequences are bi-level sequences consisting of values 1 and -1. Therefore, this property makes the sequences largely immune to the background noise. Impulse response of the system can be computed based on individual responses to Golay sequences. It turns out that:

h_cs(n) =  const . ( xcorr(Golay_A, response_to_Golay_A) + ( xcorr(Golay_B, response_to_ Golay_B),          (1)

where h_cs(n) is an estimation of the impulse response obtained via Complementary Sequences, and response_to_ Golay_{A,B} sequences are responses of the LTI system to  Golay_{A,B}  sequences, respectively. It is also interesting to observe that:

Golay_δ  = xcorr(Golay_A, Golay_A)  +  xcorr(Golay_B, Golay_B),                                                             (2)

is proportional to the Diract delta.

Note that similar benefits coming from the Complementary Sequence noise immunity can be obtained when using Maximum Length Sequences (MLS).

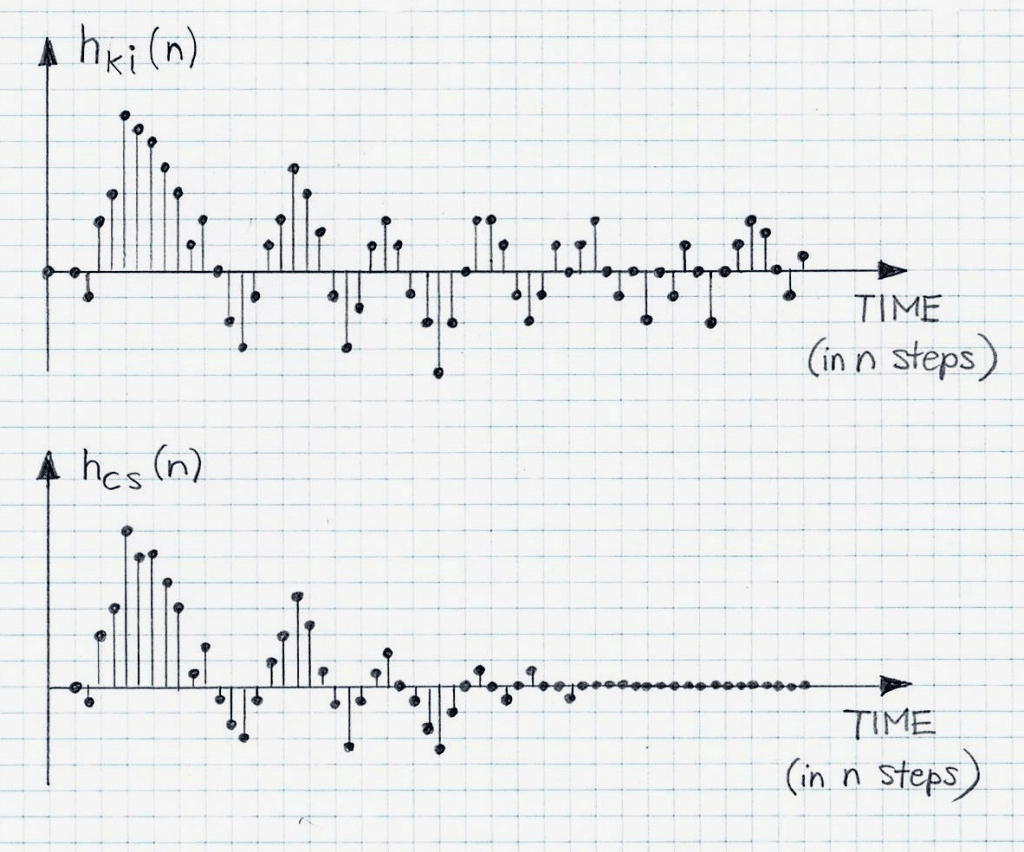
Figure 4 provides a conceptual illustration of result differences between the impulse excitation approach and the complementary sequence approach to impulse response estimation. Estimated {h_ki(n)}, n=0,1,2,…,N_max-1 is produced using the impulse excitation method with low repetition number k. Estimated {h_cs(n)}, n=0,1,2,…,N_max-1 is produced using Golay sequences. Note that a similar estimation can be produced using Maximum Length Sequences.

VOCAL Technologies engineering practices use a variety of tools and methods, including those described herein, for characterization of LTI systems. Contact us to discuss your audio application requirements.

More Information

• Echo Cancellation Design