Development and implementation of acoustic noise reduction algorithms based on Beamforming (BF) and Blind Signal Separation (BSS) require numerical simulations in order to choose the best microphone configuration for the given application. Simulation models require the mixing function linking the sound sources and sensors/microphones for the given acoustic scene be known before hand. Therefore, it is important from the R&D viewpoint to apply efficient methodology to experimentally generate the required mixing functions.
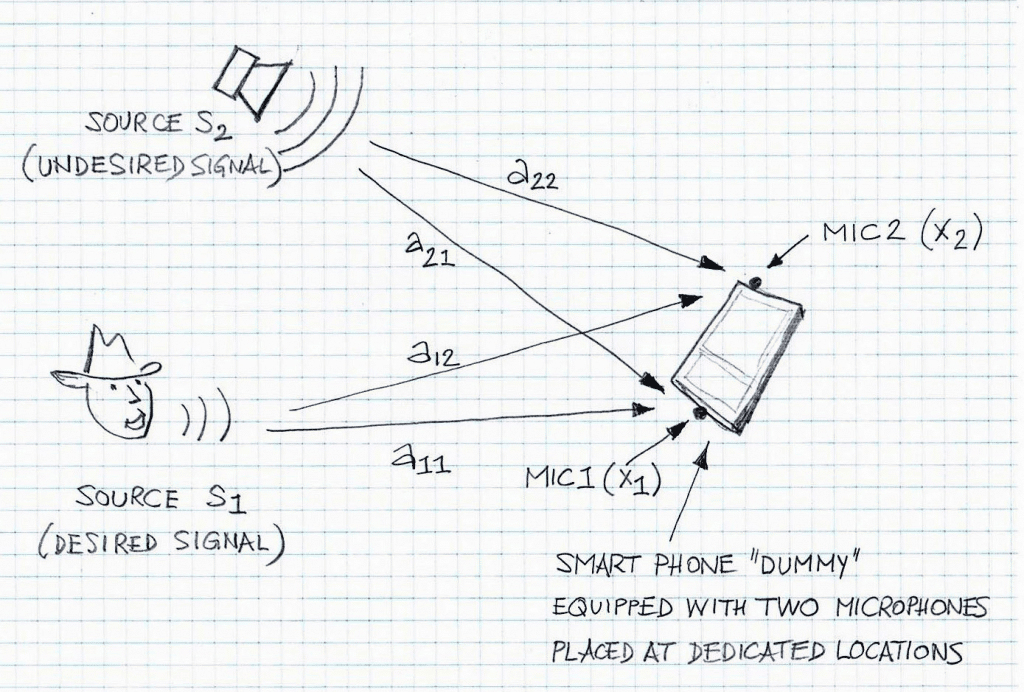
Figure 1 illustrates an acoustic scene with highlighted mixing functions (a11, a12, a21, and a22). Note that there is a short article entitled “BLIND SOURCE SEPARATION FOR NOISE REDUCTION IN MOBILE” that discusses related aspects from the viewpoint of BSS-based NR.
The mixing matrix A is essentially an impulse response matrix, with individual impulse responses aij, where i and j identify the input and output. In the case of two sources and two microphones, the size of matrix A is [2 x 2]. In general case, matrix A can be of size [M x N], where M is the number of sources and N is the number of sensors/microphones. Note, if N is greater than or equal to M, then this is consider a determinable problem. Otherwise, it is considered an undetermined solution and a different class of algorithms need to be applied.
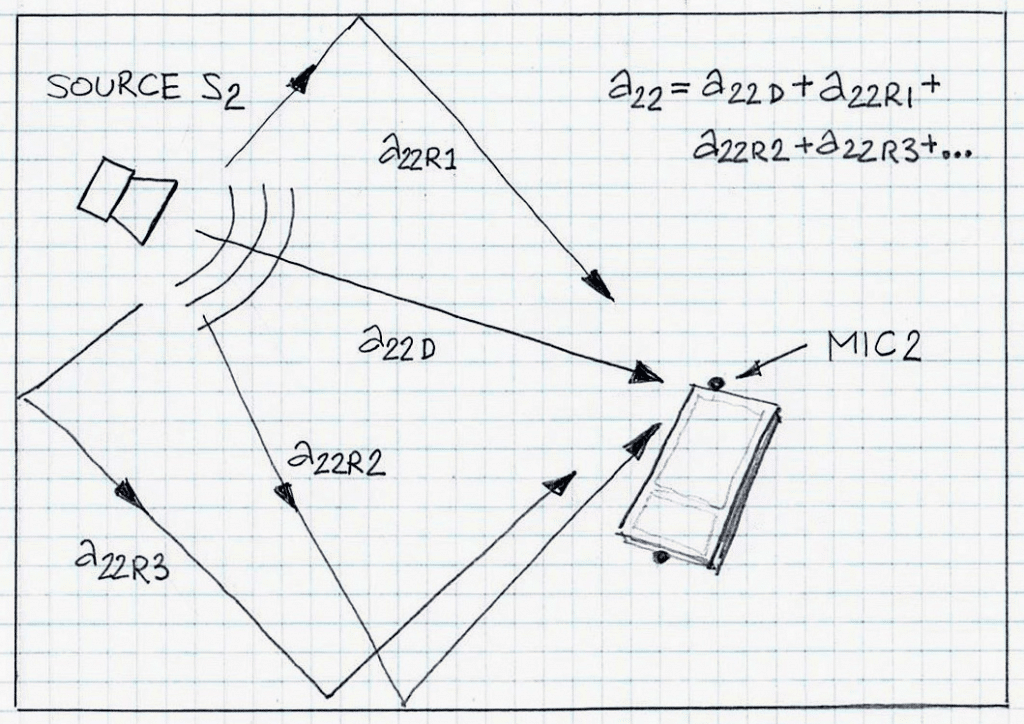
Since aij are impulse responses with i input (source si, i=1,2) and j sensor/microphone (xj, j=1,2), then the individual arrow in Figure 1 represent only relationship ‘source index vs. sensor/microphone index’; more descriptive illustration is in Figure 2, with emphasis on case a22.
Out of several possible methodologies of experimentally generating the impulse response for the mixing matrix A, here only two of them are illustrated, namely:
- Method I based on the direct generation of impulse response by using a long train of Dirac delta pulses, and
- Method II based on the use of Golay Complementary Sequences.
Figure 3 illustrates both approaches. (Please note that more information about the Golay Complementary Sequences is in article entitled “ON IMPULSE RESPONSE ESTIMATION FOR AUDIO VIA COMPLEMENTARY SEQUENCES”).
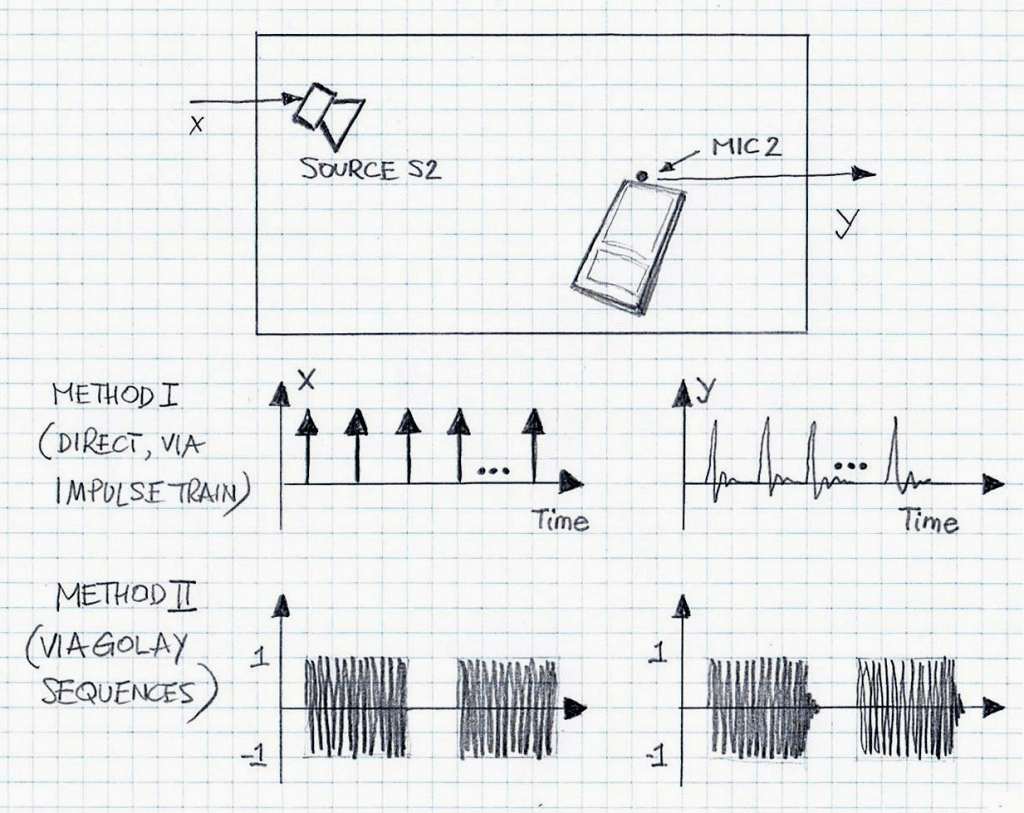
Figure 3 illustrates two methodologies/methods applied for generating matrix A. Only the case a22 is explicitly shown. Note that Method I employs a long train of pulses used as the excitation signal (the number of pulses applied can as great 500 or greater, depending of the desired accuracy); Method II employs only two noise pulses, i.e., Golay sequences, and typically no repetitions are required to generated the impulse responses (aij) with adequate accuracy.
Estimation of impulse responses of audio devices and acoustic systems requires careful statistical processing of data in order to minimize adverse effects of background noise.
VOCAL Technologies engineering practices include generation of mixing matrix components for the purpose of numerical simulations of (BF) and Blind Source Separation (BSS) approaches to noise reduction. Contact us to discuss your audio application requirements.