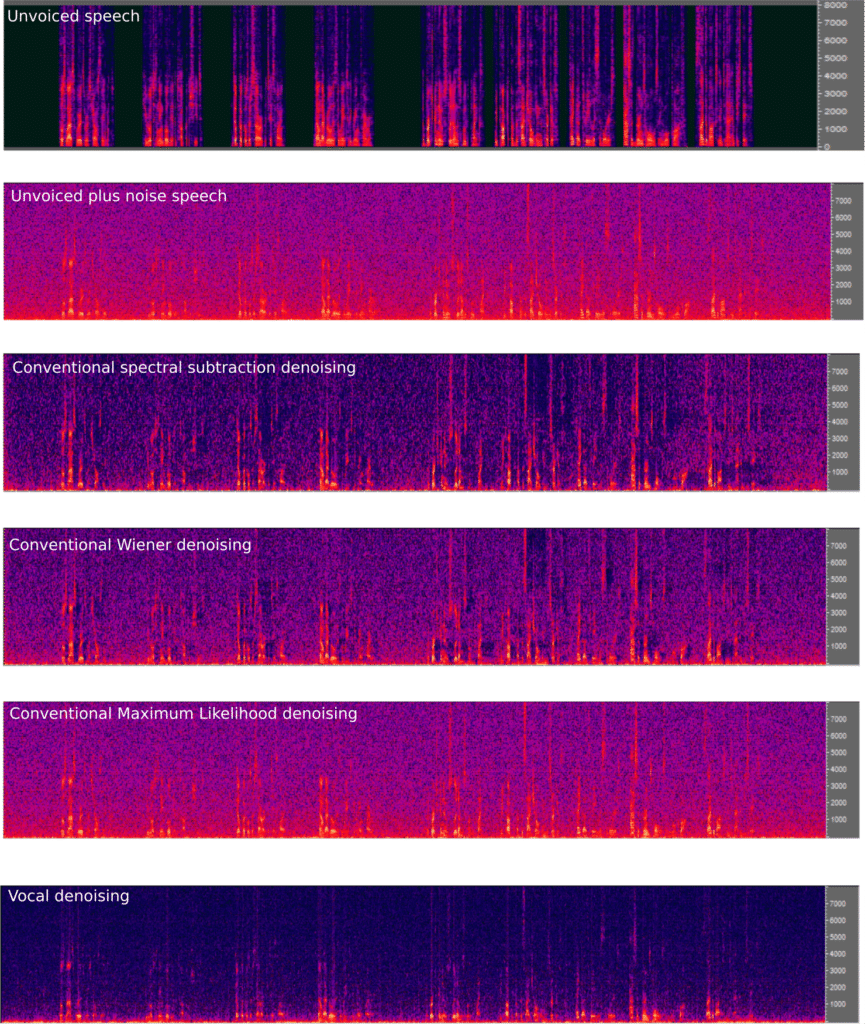
Single microphone speech enhancement based on apriori signal to noise ratio. In some real life applications, there is only a single microphone being deployed which takes off the table any potential signal to noise ratio (SNR) improvements that could have been obtained from multiple microphone beamforming. The true SNR, sometimes refered to as the apriori SNR, is most times assumed unavailable leading to the use of posteriori SNR which is the ratio of the received noisy signal power to the background noise power. Conventional approaches such as spectral subtraction, Wiener, maximum likelihood and McAulay & Malpass all use the posteriori SNR with the estimate of the noise power done during the noisy speech frames. We present an alternate whose performance surpasses all the above conventional approaches under the assumption that the background noise is complex Gaussian in the spectral domain.
Consider the single microphone speech signal:
Also suppose that a noisy estimate of the background noise is known, denoted . Then it is easy to show the sub-band cross coherence between a received frame and the noisy estimate should obey:
where is the apriori SNR,
is the noise cross coherence and
denotes real. The estimated
can then be used in any spectral based noise reduction approach. We compare the results of this approach to conventional approaches, illustrated in Figure 1 below with no nonlinear filters applied.
Figure 1: single microphone with complex Gaussian noise denoising
It can be seen on Figure 1 that this approach does far better than conventional approaches in removing the noise across sub bands.
VOCAL Technologies offers custom designed solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!