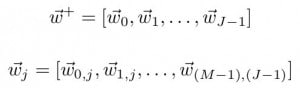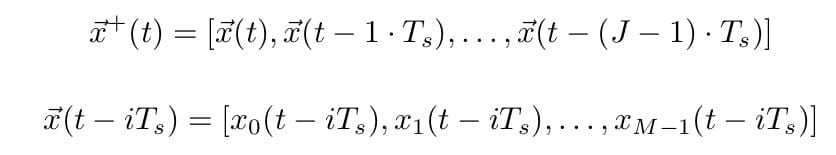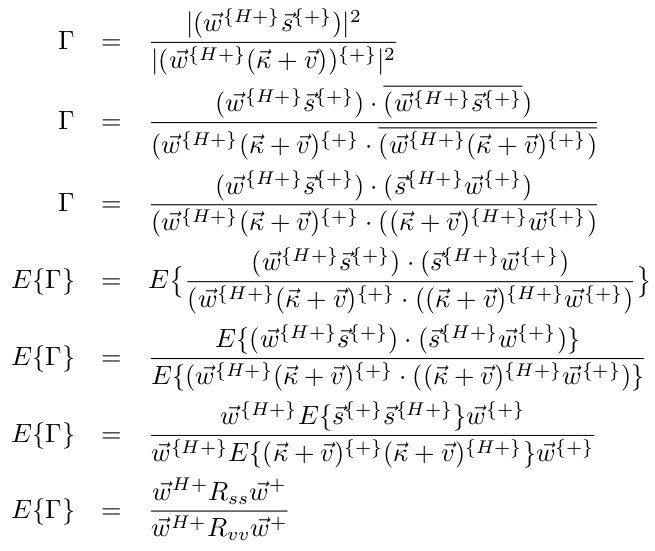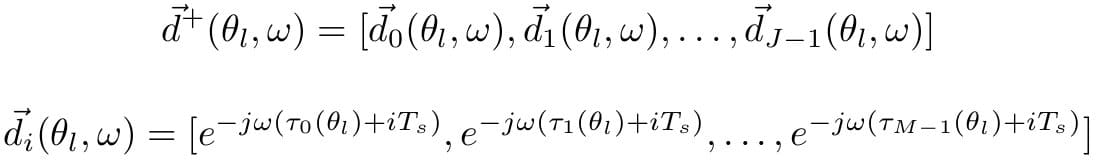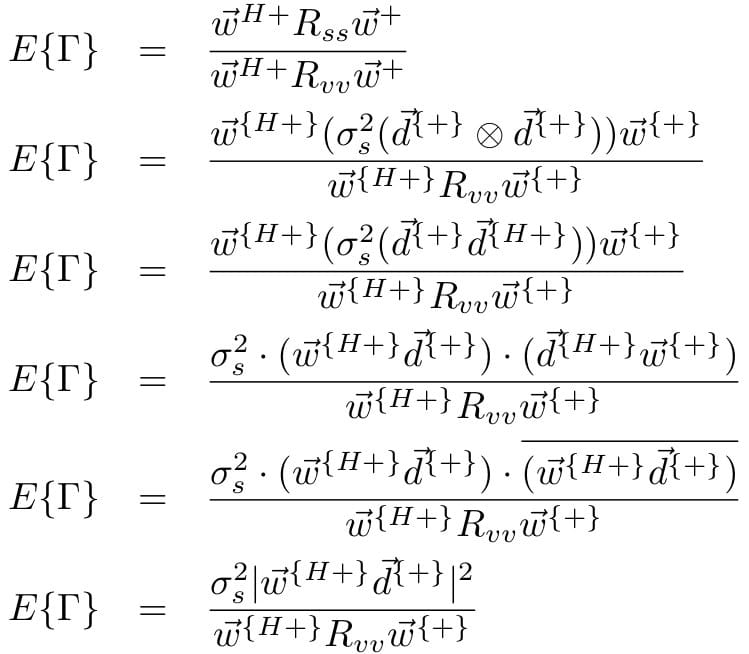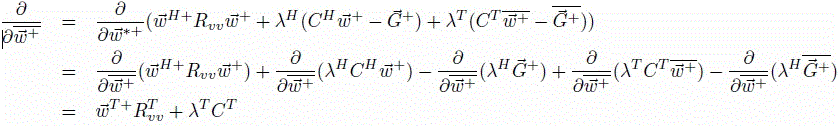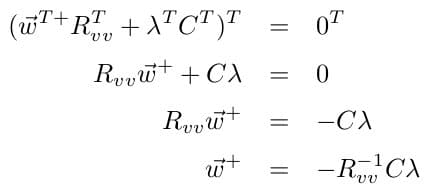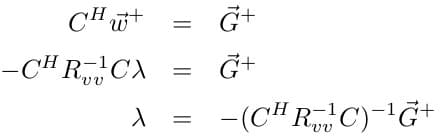VOCAL’s Broadband Constrained Minimum Variance Beamformer solution offers optimal noise reduction for speech quality enhancement applications in terms of maximizing the Signal to Interference Ratio (SINR). Our algorithm minimizes the noise power, thus minimizing the variance of the output with respect to the speech signal VOCAL’s Minimum Variance Beamforming solution is extremely robust to give you the best possible speech quality enhancement in even the most challenging environments.
We discuss how to derive this problem and find the optimal solution. For more detailed information or to discuss your beamforming application requirements, please contact us directly.
Problem Derivation
The output of our beamformer can be represented via:
Where ѡ→+ is our beamformer weight vector, which is:
Where J is the number of taps per microphone FIR filter, and M is the number of microphones. In other words, each ѡ→i holds the ith tap weight for each microphone m. Similarly, we aggregate our microphone signal as:
Where Ts is the sampling period, so that x→(t– iTs) holds the data point on the ith tap of each microphone m. Our microphone signal is assumed to be of the form:
Where s→m(t) = s(t) e jѡ (t-(Τm(Ɵ) + iTs)), km and vm are statistically independent signal, interference, and noise at the mth microphone. The term e jѡ (t-(Τm(Ɵ) + iTs)) is our model for a complex plane wave arriving from angle Ɵ at the ith sampling instant. Our optimal ѡ→+ is found by maximizing the signal power with respect to the noise and interference power:
Where Rss and Rvv represent the autocorrelations of the signal and interference plus noise respectively, and ![]() represents complex conjugation. To maximize this function, we want to make the denominator small. Hence, our objective function becomes:
represents complex conjugation. To maximize this function, we want to make the denominator small. Hence, our objective function becomes:
At the same time, we can make the numerator large. Hence we introduce a constraint:
Essentially, this says that we are gaining our desired signal power ѡ→H+Rss ѡ→+ by G. For our beamformer, we want to pass the signal coming from Ɵl with frequency ѡ with a power gain G, while minizing the noise power. Therefore, our constraint is written as:
Where d→+(Ɵl, ѡ) is our array manifold vector, which describes how the beamformer will respond to our signal model, the plane wave, arriving from angle Ɵ with frequency ѡ. It is written as:
In fact, this is entirely equivalent to our previous constraint, because in the special case of a point source signal we have:
Where ![]() denotes the outer product. In other words, we can represent our power ratio as:
denotes the outer product. In other words, we can represent our power ratio as:
Hence, we still want to make the denominator small and the gain the numerator to a large value G. Hence our optimization problem becomes:
Solution Derivation
Going further, we will use the notation CH = d→H(Ɵ→l, ѡ→). The solution to this optimization problem can be found by first forming the Lagrangian:
Due to the quadratic form ѡH+ Rvv ѡ→+ present, this function is clearly convex, therefore if we set the derivative equal to zero and solve, we will assuredly obtain the global minimum:
The minimum is then found:
Since the constraint equation says CH ѡ→+ = G→+ , we plug in ѡ→+ from the above result into this constraint equation to obtain:
Hence, we plug in our result for λ into ѡ→+ = -R-1vv Cλ :
Hence our solution is: