Beamforming techniques are highly enhanced based on a-priori knowledge of the noise/interference direction of arrival. Techniques to estimate the noise direction of arrival depend on the number of sensors for improved accuracy. However, in most cases, due to the form factor of the device, only two sensors are deployed with a small separation distance on orders of . Some applications, thankfully, do not require exact angle of arrival information because any estimate with “good” proximity to the true direction of arrival will do. In such situations, coherence based approaches can be deployed.
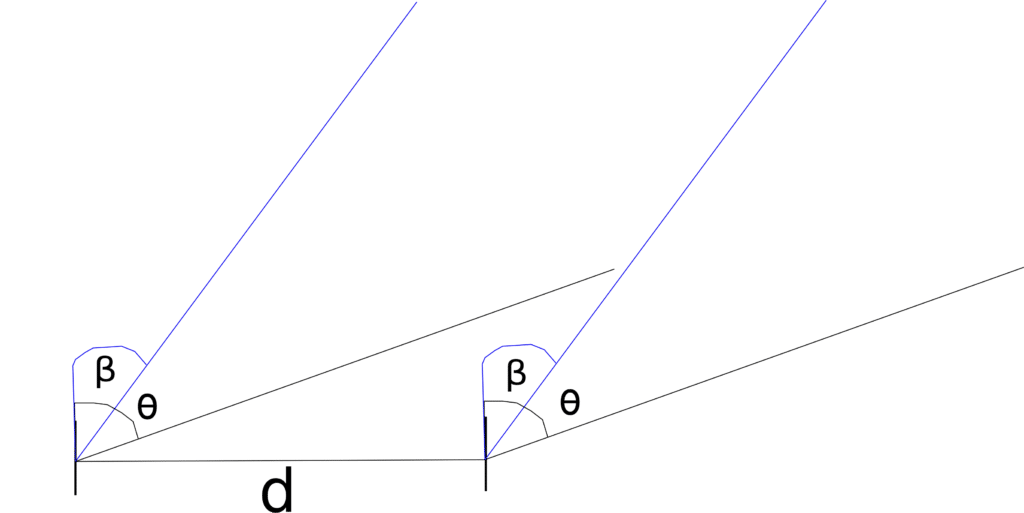
Consider a far field acoustic signal impinging microphones with separation distance
at an angle of
and an inference signal impinging at an angle
. The signal at microphone
,
, can be denoted as
where is the delay of the desired signal at microphone
,
is the delay of the noise signal at microphone
,
is the source signal,
is a the noise and
is the speed of acoustic signals. Both
and
are zero mean ergodic processes. We will like to cancel out the interfering signal
and beamform
. The setup is as shown in Figure 1.
Two microphones with pairwise distance of
The so called coherence between the signals recorded at the two microphones, is given by:
where and $latex\alpha_1(\omega) = SNR(\omega)$.We can use the sign of the imaginary portions of the coherence, thus, sign of
,to do selective filtering if we already know, or have an idea, of the look direction of the desired signal. Deployment of such a filter can be utilized to select
separated dual signals as shown in Figure 2 below.
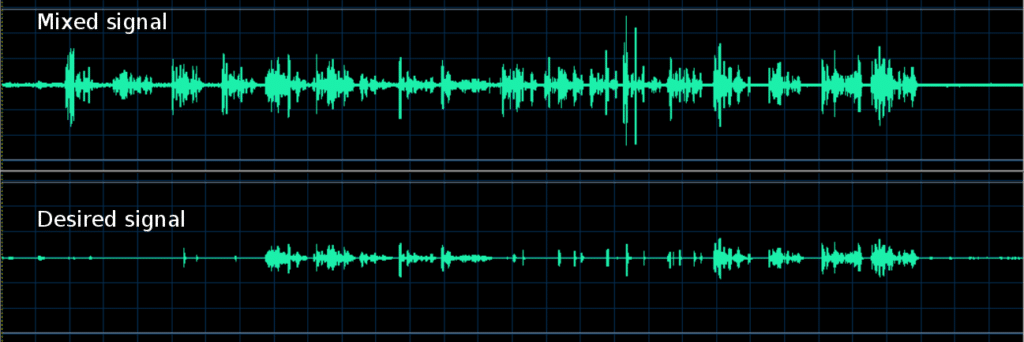
Example of using coherence based method for signal separation
VOCAL Technologies offers custom designed AoA estimation solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!