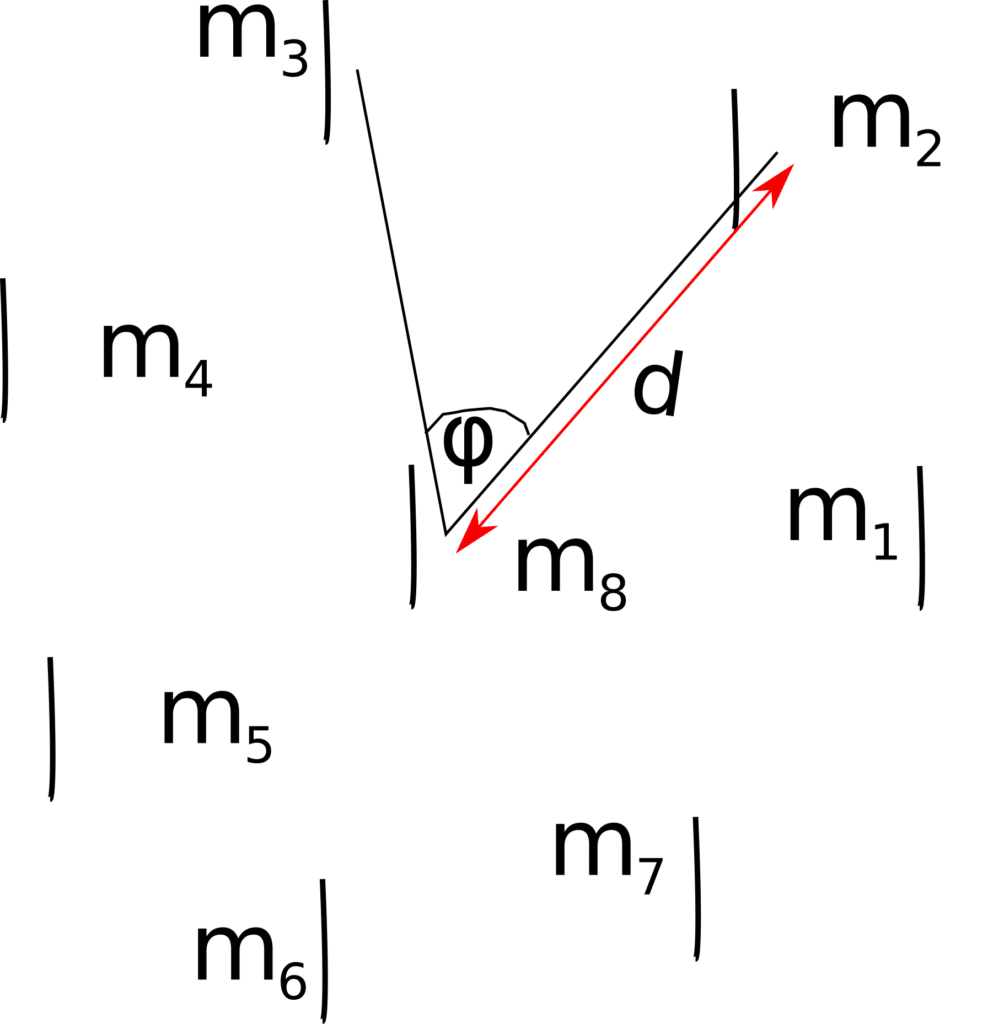
We describe an approach to beamforming an acoustic source with a circular array microphone topology by deploying a single inverse filter which is source direction blind. Consider the circular array illustrated in Figure 1 below and suppose a beamforming solution is desired.
Figure 1: Circular microphone array topology for 8 microphones, $latex \psi= \frac{2\pi}{7}$.
Define the angle of arrival of the signal from a source at $latex s$ to be $latex \theta$, the impinging angle at microphone $latex m_{8}$ using the line joining microphones $latex m_k$ and $latex m_8$ as reference such that the following holds:
$latex \theta = \underset{\left| \angle {\left(m_k,m_8, s\right)} \right|}{\arg\max} \angle{\left(m_k,m_8, s\right)}$
It is easy to visualize then that for all signals arriving from a $latex 360^{\circ}$,
$latex -\frac{\psi}{2} \le \theta – \frac{\pi}{2} \le \frac{\psi}{2}$
Thus, for all direction of arrivals, $latex \exists \theta$, $latex -\frac{\psi}{2} \le \theta – \frac{\pi}{2} \le \frac{\psi}{2}$ such that :
$latex Y(w) = X_{\theta} (w) H_{\theta}(w) + \frac{1}{8}\sum\limits_{n}^8 N_n(w)$
$latex H_{\theta}(w)$, the effective “sum filter”, can be synthesized as:
$latex H_{\theta} (w) = \frac{1}{8} + \frac{1}{8} e^{-j w \frac{d}{d} \sin{\theta}} + \frac{2}{8} \sum\limits_{n=1}^3 e^{j w \frac{d}{c} \cos{(n\psi)} \sin{\theta}} \cos{\left( w \frac{d \sin{(n \psi)}}{c} \sin{\theta} \right)}, -\frac{\psi}{2} \le \theta – \frac{\pi}{2} \le \frac{\psi}{2}$
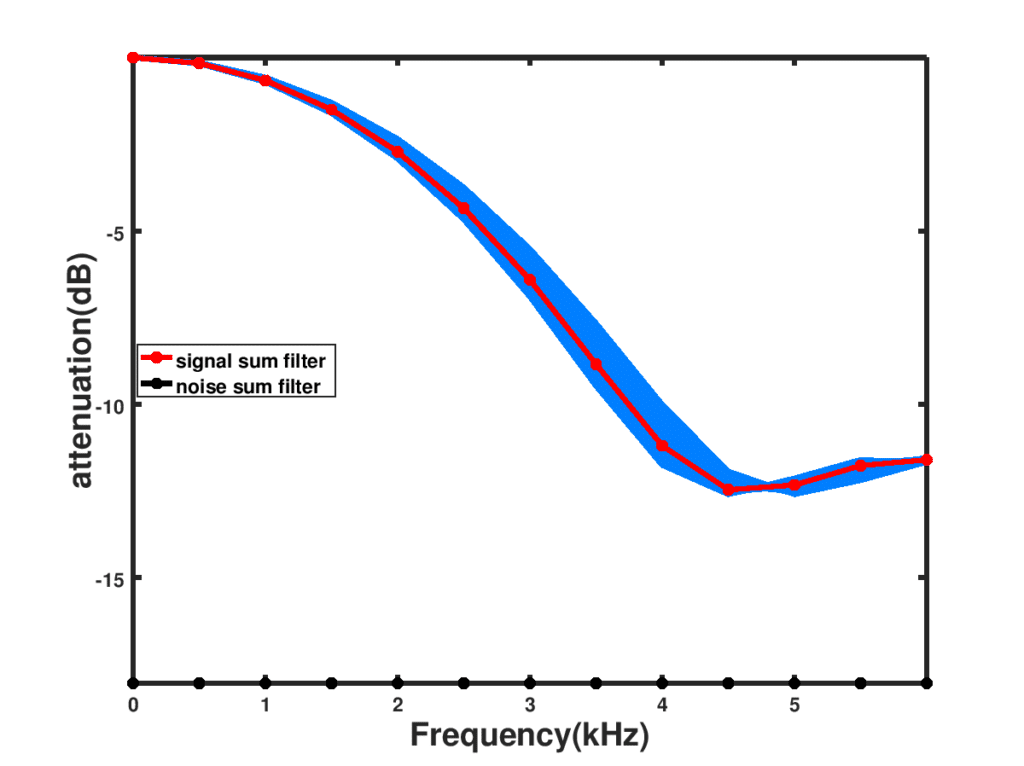
$latex H_{\theta}(w)$, the filter arising from summing the signals at all microphones, attenuates some speech signals considerably as seen in Figure 2 below, and has to be compensated for.
Figure 2: Filter produced by summing all the microphone outputs.
To remove the effects of the filter $latex H_{\theta}(w)$, we need knowledge of $latex \theta$. This requires computing the direction of arrival with its accompanying error margins and picking the appropriate inverse filter to apply. In real time operating systems, this requirement may overwhelm the processor. An alternative exists such that there is no requirement to actually know the direction of arrival of the signals and only a single inverse filter is required. This alternative hinges on the previous stated observation that:
$latex \theta = \underset{\left| \angle {\left(m_k,m_8, s\right)} \right|}{\arg\max} \angle{\left(m_k,m_8, s\right)}$
Suppose we assume the direction of arrival is $latex \theta = \frac{\pi}{2}$, how much error will the magnitude response pick up due to the error margin within $latex \pm \frac{\psi}{2}$ in $latex \theta$ ? It turns out the errors in the scaling is very minimal; no more than $latex 2dB$. Thus we can apply an inverse filter of
$latex \hat{H}_{\theta}^{-1} (w) = \frac{1}{H_{\theta}(w)}$
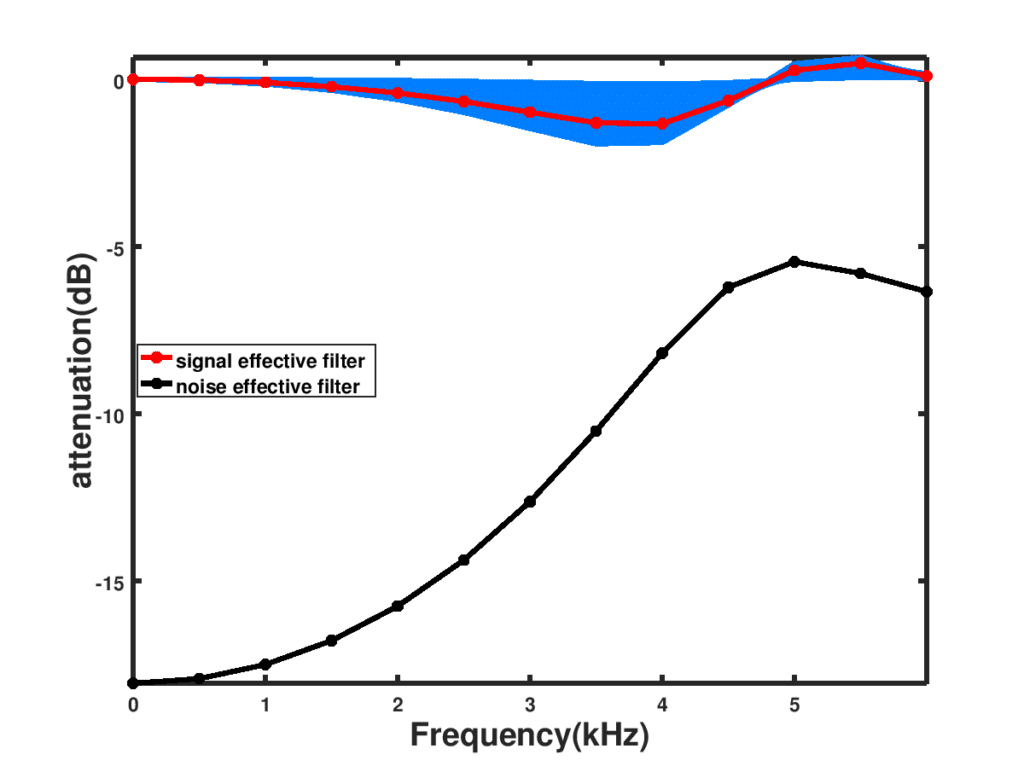
The effective magnitude response of the above approach, $latex \forall ~ \theta$, is as shown in Figure 3 below:
Figure 3: Effective filter magnitude response
The super directivity of the filter can be used to improve the noise attenuation.
VOCAL Technologies offers custom designed solutions for beamforming with a direction of arrival estimation, robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!