Speech Enhancement w/ Multi-Mic Noise Reduction

The application of microphone array beamforming to coherent noise fields is well documented and researched. Minimum Variance Distortionless Response (MVDR) beamforming and Generalized Sidelobe Canceller (GSC) are the most popular methods for attenuating coherent interfering noise sources with a determinable direction, such as a television or another human talker in the same acoustic environment. However, in a diffuse noise field the noise sources are considered non-localized with an undeterminable direction. The wind noise cause by the friction of the air with a car or an airplane as can be considered a diffuse noise source inside the vehicle. Especially in aeronautical applications, this noise component can be quite strong. Since, the diffuse noise has no direction the spatial filtering and characteristics provided by the MVDR and GSC methods will have limited improvement to the Signal-to-Noise Ratio (SNR).

There are two main multi-mic noise reduction methods for improving the results of linear beamforming:

Introduce a noise reference signal
Utilize a beamforming post-filter

Both of these methods generate a gain function to be applied to a noisy signal. For this article case our desired signal is speech. Speech is a wideband non-stationary sound source, so the gain function will be calculated in the frequency domain utilizing the Short-Time Fourier transform (STFT). In other words, the gain function is to be calculated for each time-frequency bin.

Speech Enhancement Utilizing a Noise Reference Signal

In a diffuse noise field, the noise is scattered about the environment in such a manner that the average energy is similar when captured at different locations. Thus, the only meaningful information of about the noise field is the time-frequency amplitude component. An amplitude-based transfer function can be use to translate the diffuse noise component captured at one microphone to another.

Given a microphone signal:

$Y_1\left(t,f\right)=S_1\left(t,f\right)+N_1\left(t,f\right)$

Where $S_1\left(t,f\right)$ and $N_1\left(t,f\right)$ are the desired speech signal and diffuse noise components at a given time-frequency, respectively.

Then a second microphone signal can be expressed as:

$Y_2\left(t,f\right)=H\left(t,f\right)\bullet S_1\left(t,f\right)+\left|A\left(t,f\right)\right|\bullet N_1\left(t,f\right)$

Where $H(t,f)$ is the transfer function of S1 between measurement points $Y1$ and $Y2$ . $|A(t,f)|$ is amplitude based transfer function of the diffuse noise from $Y1$ signal.

In order to use $Y2$ as a noise reference signal, the $H(t,f)$ needs to minimize the component of $S1$ . There are two paths to achieve this design goal.
The first option is to nullform or spatially filter the desired signal utilizing a co-located microphone array. Just as in the GSC approach, implementing a blocking matrix to will remove the desired signal leaving the noise components behind. This option can be applied to near-field and far-field applications, but requires sufficient tracking of the desired source signal. As nullforming is sensitive to estimation errors of the directional of arrival, which will lead to leakage of $S1$ into the $Y2$ signal.
Alternatively, since, speech can be modeled as point sound source, the distance effect does apply. If the sound source is in the near-field to original microphone (approximately less than 1 meter), a noise reference microphone can be placed a sufficient distance from the desired sound source to minimize its presence in $Y2$ . The distance effect states that each doubling of distance halves the sound pressure level, a 6dB reduction.
Assuming S1 has been sufficiently removed from the noise reference signal (i.e. $H(t,f) -> 0$ ) through nullforming or the distance effect. The multi-mic noise reduction gain function can be written as:
$g\left(t,f\right)=\ \frac{Y_1\left(t,f\right)-Y_2\left(t,f\right)}{Y_1\left(t,f\right)}=\ \frac{\left(1-H\left(t,f\right)\right)S_1+\left(1-\left|A\left(t,f\right)\right|\right)N_1}{S_1+N_1}$

We are now left to estimate amplitude gain factor $|A(t,f)|$ . Diffuse noise when compared to speech can be considered stationary. Therefore, decision-direct approach using a long term recursive moving average can be use to determine this component of the system.

Speech Enhancement Utilizing a Beamforming Post-Filter

MVDR and GSC beamforming provide limited SNR improvements in the diffuse noise fields without correlated noise sources. The basic assumption of beamforming post-filter in a diffuse noise field is the desired speech signal is mutually correlated among microphone signals, while the noise components are uncorrelated.

There are a multitude of ways to used this information. One STFT beamforming post-filter design is based on the ratio of the output power of the beamforming with the input signal power. This gain function is:

$g\left(t,f\right)=\frac{P_{BF}\left(t,f\right)}{P_{IN}\left(t,f\right)}$

Since, the goal of most beamformer designs is provide unity gain in the direction of the desired signal, this post-filter will have $g\left(t,f\right)\approx1$ when the time-frequency instance contains speech, and $g\left(t,f\right)<1$ , when the time-frequency instance contains noise.

Similarly, the Zelinski post-filter is an adaptive Post-Filter using the auto and cross spectral densities. This gain function is defined as:

$g\left(t,f\right)=\frac{\frac{2}{M\left(M-1\right)}\sum_{i=1}^{M-1}\sum_{j=1}^{M}{Y_i\left(t,f\right)\bullet Y_j\left(t,f\right)}}{\frac{1}{M}\sum_{i=1}^{M}{Y_i\left(t,f\right)\ast Y_i\left(t,f\right)}}$

When the average cross spectral density is approximately equal to the average power spectral density, this indicates the presence of the desired speech signal, $g\left(t,f\right)\approx1$ .

It cannot always be assumed that the output of a beamformer and/or the inputs of the microphones consist entirely of diffuse noise components. A more general Wiener post-filter design is as follows:

$S_s-g_{opt}\bullet S_y=0$
$g_{opt}=S_s/\left(S_s+S_n\right)=\left(S_s/S_n\right)/\left(S_s/S_n+1\right)$

This post-filter design does require the estimation the speech and noise power of the beamforming input signals. The design goal of this spatial noise suppression filter is the same as the traditional MMSE noise suppression. You want to minimize the error between the estimate desired signal and the desired signal. Since, the actual desired signal is unknown the average (a-priori) and the instantaneous (a-posteriori) SNR values need to be estimated. Again, a decision-direct approach can be used to estimate noise and speech signals. With a microphone arrays signal processing, you do not have to solely rely on a voice activity detection decision. Instantaneous Direction of Arrival estimation can be used to determine if the signal energy is arriving from the desired sound source or an interfering noise source. This information can be used in conjunction with cross-spectral density to estimate the SNR.

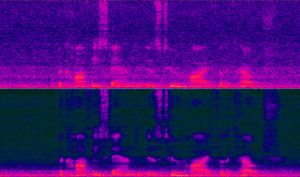
The image below shows the spectrogram of the before (top) and after (bottom) beamforming with a post-filter in a diffuse noise field.

As described in this article, the utilization of multiple microphones in a product design opens up a multitude of possibilities to overcome the limitations of traditional single channel noise suppression solutions. We look forward to discussing how VOCAL can apply our algorithms and expertise to your product design.

Complete Communications Engineering

Speech Enhancement w/ Multi-Mic Noise Reduction in Diffuse Noise Field

Speech Enhancement Utilizing a Noise Reference Signal

Speech Enhancement Utilizing a Beamforming Post-Filter

More Information