Linear Constrained Minimum Variance (LCMV) Beamforming

Linear constrained Minimum Variance (LCMV) beamforming is a technique widely used in multi-channel acoustic signal processing. It is general enough to form a common framework to design beamforming algorithms for various physical setups.

The following diagram displays the acoustic interconnection between M sound sources and N microphones in a sound field.

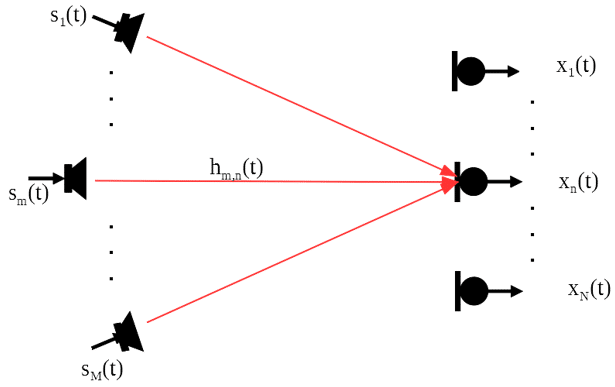
Each microphone captures a combination of the M sources through an acoustic impulse response. We use the subscripts {m, n} to denote the impulse response path from source m to the microphone n.

The captured sound for the n’th microphone

$latex x_n\left(t\right)=\sum_{m=1}^{M}{h_{m,n}\ast s_m\left(t\right)}$

$latex \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\sum_{m=1}^{M}\sum_{l=0}^{L-1}{h_{m,n}\left(l\right)s_m\left(t-l\right)}$

A more general approach is to apply filtering for each of the microphone signal and sum into a recovered estimation for each source. The following diagram describes the process. The filter for the n’th microphone to the recovered source y_p(t) is denoted by w_n,p(t).

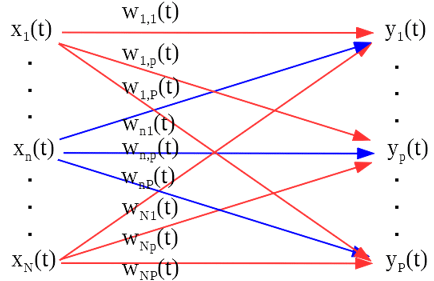
The recovered source sound can be written as below.

$latex y_p\left(t\right)=\sum_{n=1}^{N}{w_{n,p}\ast x_n\left(t\right)}$

$latex \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\sum_{n=1}^{N}\sum_{j=0}^{J-1}{w_{n,p}\left(j\right)x_n\left(t-j\right)}$.

The filtering coefficients for each of the microphone can be optimized with some objective functions. We further write the array output as below.

$latex y_p\left(t\right)=\sum_{n=1}^{N}\sum_{m=1}^{M}\sum_{j=0}^{J-1}\sum_{l=0}^{L-1}{w_{n,p}\left(j\right)h_{m,n}\left(l\right)s_m\left(t-l-j\right)}$

Assume that we desire only to recover the first source s₁ and all the other sources are considered as interference signals.

$latex y_0\left(t\right)=\sum_{n=1}^{N}\sum_{j=0}^{J-1}\sum_{l=0}^{L-1}{w_{n,p}\left(j\right)h_{1,n}\left(l\right)s_1\left(t-l-j\right)\ +}$

$latex \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\sum_{n=1}^{N}\sum_{m=2}^{M}\sum_{j=0}^{J-1}\sum_{l=0}^{L-1}{w_{n,p}\left(j\right)h_{m,n}\left(l\right)s_m\left(t-l-j\right)}$

Obviously, the first term contributes to the useful information about the first source and the second term accounts for all interference sources. Ideally, we would like to have our beamforming processing to have the following effect.

$latex y_0\left(t\right)=s_1\left(t-\delta\right)$

and

$latex \ \ \ \ \ \ \ \ \ \sum_{n=1}^{N}\sum_{m=2}^{M}\sum_{j=0}^{J-1}\sum_{l=0}^{L-1}{w_{n,p}\left(j\right)h_{m,n}\left(l\right)s_m\left(t-l-j\right)} = 0$

where $latex \delta$ is a simple delay. The beamformer would have perfect equalization on source one and complete cancellation on the other interference sources. The interference sources are perfectly separated from the target source. We refer to the scenario as spatially separable beamforming.

Spatially separable beamforming is rarely possible in reality. Therefore, we usually use some priori knowledge about the target sound source. The priori knowledge may be location or direction information from which we can formulate constraints on the beamforming vector $latex {w}_{n}\left(j\right)$.

For example, we may want to constrain that the first microphone signal comes through without distortion,

$latex {w}_1\left(t\right)={\delta}\left(1-p\right)$

In general, we may formulate the constraints into a matrix form,

$latex C^Tw\left(p\right)=c$

where c is the desired vector derived from the priori knowledge of the source and C denotes a linear matrix which forces $latex {w}\left(p\right)$ into the desired vector c.

Therefore, after imposing the linear constraint from the priori knowledge of the target source, we can rewrite the beamforming problem into the following optimization,

$latex {\underset{w\left(p\right)}{min}}E\{y^2\left(p\right)\}$

subject to: $latex C^{T{w}}\left(p\right)={{c}}$

With some mathematics, we reach the following standard solution,

$latex {{w}}=R_{xx}^{-T}C^T\left(C^TR_{xx}^{-T}C^T\right)^{-1}{{c}}$.

The above approach is in general referred to as linear constraint minimum variance (LCMV) beamforming algorithm. However, the use of LCMV is not often so straight forward.