Precise location estimates of sound sources are becoming important in many applications such as gaming, beamforming and conferencing. In most of these applications, a half-plane resolution is required since, for example, in gaming applications, the the user stands in front of the device only. This has led to many gadgets employing a linear array of microphones. The combination of the sensors to estimate the location of the source leads to many different algorithms. Many of the existing algorithm combine the signals at the senors to achieve a resolved angle of arrival of the signal. The approach employed here assumes that the incident angle at all the senors are identical since a far field assumption is used. We present an alternate which does not make this assumption and can be used for both far field and near field models and further produce a closed form solution devoid of searching over a grid.
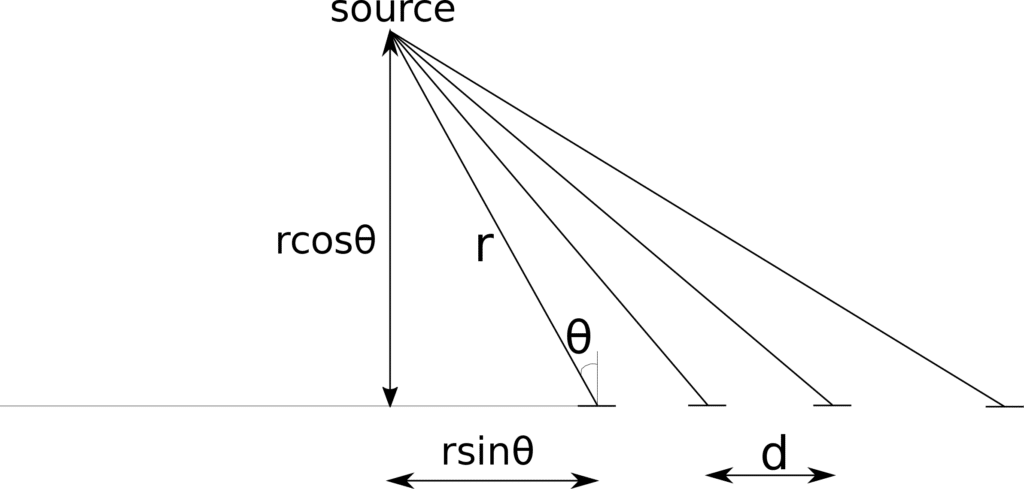
Figure 1: M ULA microphones
The pair-wise time difference of arrival, can be obtained using GCC-PHAT, SRP-PHAT, coherence, or any optimal algorithm for an particular application. Note that, even though these approaches, GCC-PHAT etc, are used primarily for angle of arrival estimations, their primary intermediate output the time difference of arrival at paired sensors before data fusion to determine angle of arrival. The range of the source from each sensor,
to
, from left to right on Figure 1 is:
Thus the pairwise time difference of arrivals obey:
We can pivot around the first microphone to reduce the equation above to
We can further resolve the angle of arrival, and inherently the source using:
Characterizing the noise in the time difference of arrival estimate as a zero mean random process for each microphone will lead to the errors in the least squares solution to the parameter approaching zero as the number of microphones become large.
VOCAL Technologies offers custom designed direction of arrival estimation solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!