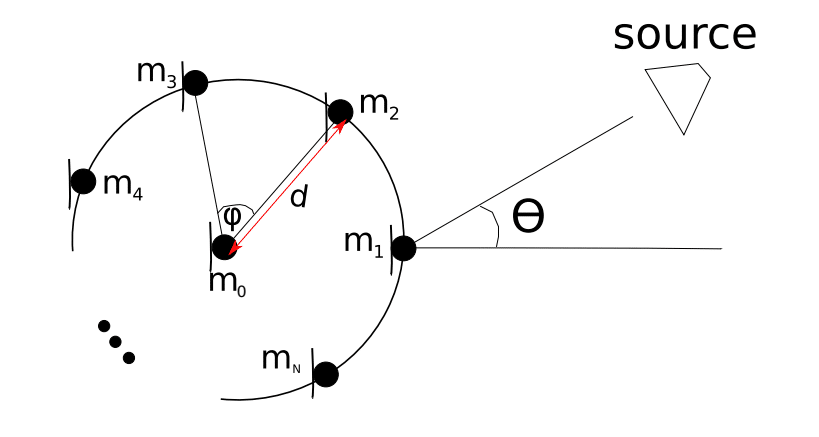
Centered circular array DoA estimation using least squares

Centered Circular Array Direction of Arrival Estimation Using Least Squares. The use of microphone arrays to estimate the direction of arrival (DOA) of sound sources is widespread. Most algorithms however are tailored for linear array topologies. A limitation of linear arrays is that they can only resolve a half plane with folding spacial ambiguities. We now consider the case of a centered circular array topology for estimating the DOA. Consider a far field speech impinging $N+1$ microphones arranged in a centered circular topology and suppose it is desired to estimate the DOA. This is depicted in Figure 1 below:

$N+1$ microphones in centered circular array

The signal at each microphone obeys:

$x_i(t) = h_i(t)*s(t - \tau_i) + \nu(t)$

where $\tau_i$ is the delay from the source and $*$ denotes convolution. Its is easy to verify that the time difference of arrivals (TDOA) will obey:

$\tau_j - \tau_0 = \tau_{0,j} = \frac{d}{c} \cos{\left((j-1)\psi - \theta\right)}, j \ge 1$ $\tau_j - \tau_1 = \tau_{1,j} = \frac{d}{c} \sin{\left((j-1)\frac{\psi}{2} - \theta\right)}, j \ge 2$

where $d$ is as shown on Figure 1 and $\theta$ is the DOA with respect to the ordinate. The angle $\psi = \frac{2\pi}{N}$ . For $N+1$ microphones, we get $\frac{N(N+1)}{2}$ unique tuples from which the TDOA can be estimated. We can however reduce it to use only the two equations above, making $2N-1$ tuples. This will lead to a system of equations given as:

$\underbrace{\begin{bmatrix}\tau_{0,1}\\\tau_{0,2}\\\vdots\\\tau_{0,N}\\\tau_{1,2}\\\vdots\\\tau_{1,N}\end{bmatrix}}_{Y} = \underbrace{ \frac{d}{c}\begin{bmatrix}0 & 1\\\sin{\psi} & \cos{\psi}\\\vdots & \vdots\\\sin{\left((N-1)\psi\right)} & \cos{\left((N-1)\psi\right)}\\-\cos{\left(\frac{\psi}{2}\right)} & \sin{\left(\frac{\psi}{2}\right)}\\\vdots\\-\cos{\left((N-1)\frac{\psi}{2}\right)} & \sin{\left((N-1)\frac{\psi}{2}\right)}\end{bmatrix}}_{A} \begin{bmatrix}\sin{\theta}\\\cos{\theta}\end{bmatrix}$

Then the least squares solution becomes

$\begin{bmatrix}\sin{\theta}\\\cos{\theta}\end{bmatrix} = (A^T A)^{-1} A^T Y$

It should be noted that $(A^T A)^{-1} A^T$ can be precomputed once and then only $2N-1$ additions and multiplications are required to estimate $\sin{\theta}$ and $\cos{\theta}$ after the time delay tuples have been estimated. Given $\sin{\theta}$ and $\cos{\theta}$ , the unique $\theta$ can be readily estimated without any spatial aliasing. The choice of sampling Frequency and/or $d$ , together with the number of microphones can be used to determine the resolution of the returned DOA. Figure 2 below illustrates and example with real speech, 8 microphones at a sampling frequency of 16kHz and $d = 0.024mm$ . The true DOA is $0$ or $360$ degrees.

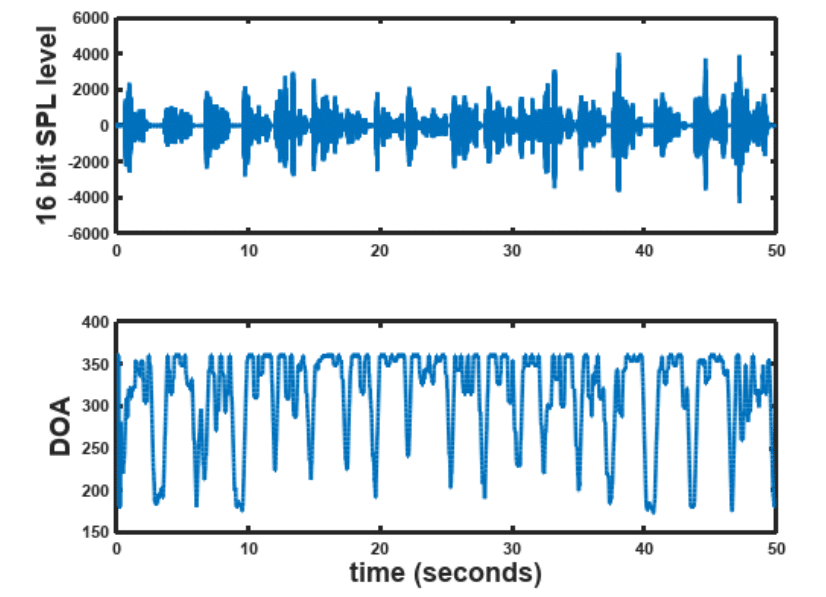
[TOP] Speech signal [BOTTOM] Estimate of the true angle of $0$ or $360$ degrees.

It can be seen that in the DOA estimate is pretty accurate. This technique can be easily extended to estimate multiple speakers if the speakers can be separated in the time-frequency domain with some binning to isolate specific DOAs.

VOCAL Technologies offers custom designed solutions for beamforming with a robust voice activity detector, acoustic echo cancellation and noise suppression. Our custom implementations of such systems are meant to deliver optimum performance for your specific beamforming task. Contact us today to discuss your solution!

Complete Communications Engineering

Centered Circular Array Direction of Arrival Estimation