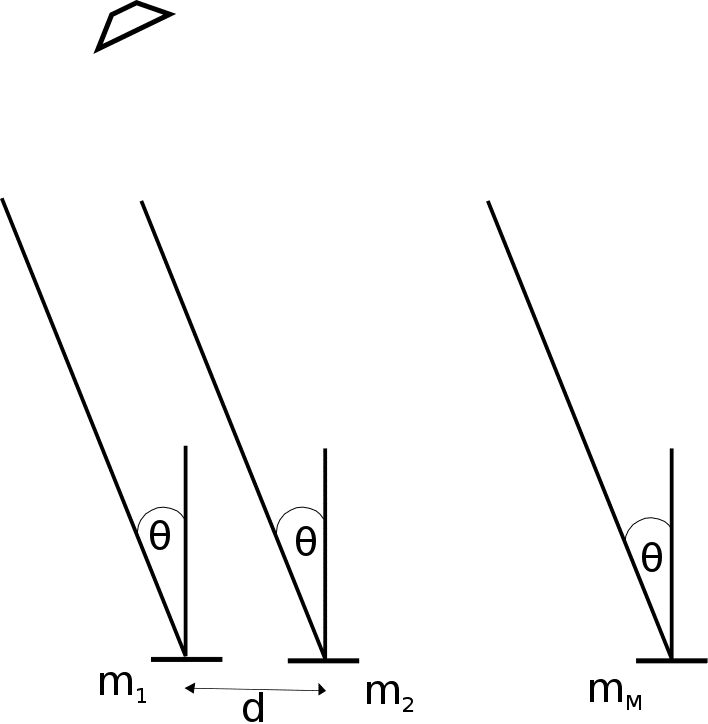
Fundamental Limits On Angle Of Arrival Estimation Error For Acoustic Microphone Array. We present a lower bound on the fundamental limits of the error margin for the angle of arrival estimation – using a finite set of linear microphone arrays – in the noise free environment. In particular, consider a far field acoustic signal impinging a uniform linear array (ULA) of microphones with separation distance
at an angle of
. Suppose the channel is stationary and free of additive noise, such that, barring channel attenuation, signals captured at all microphones are identical up to a scaling parameter plus sample delays. The signal at microphone
,
, can be denoted as
, where
is the channel impulse response,
denotes convolution,
is the delay at microphone
and
is the source signal. The setup is as shown in Figure 1 below.
Figure 1: ULA of microphones with pairwise distance of
We will like to quantify the maximum error in the angle of arrival estimates given a sampling rate of . Suppose the estimated angle of arrival is
, then the estimated error will be given by:
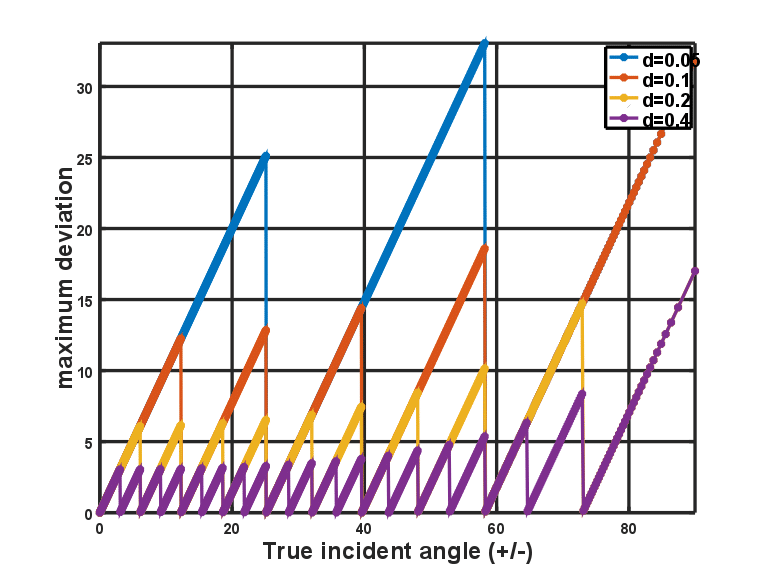
where denotes the floor operator. Error margins for various incident angles are illustrated in Figure 2 using
and values of
.
Figure 2: Lower bound on angle of arrival estimation errors.
Figure 2 illustrates that increasing the separation between paired microphones reduces the margin of errors significantly. It should however be noted that the larger the separation, the more flawed the assumption of the acoustic source signal impinging all microphones at a common angle is. Thus, in real applications, the engineer would need to chose as a design parameter to optimize a specified criteria.