Adaptive Null Steering Algorithms

A microphone array can also be used to suppress an interference sound source in addition to enhance the target sound source. This short article introduces an algorithm that remove or suppress interference sound sources while preserving the desired target sound.

As shown in the diagram below, two sound sources are present, the target sound at 0 degree angle and interference sound at 60 degree angle. Let $g\left(w,\theta\right)$ be the gain function of the beamforming vector w and the direction $\theta$ .

Figure 1: Beamforming Gain Function $g\left(w,\theta\right)$

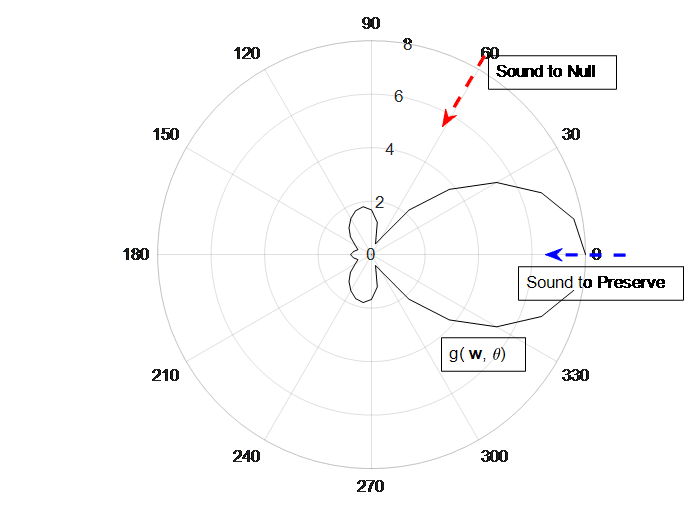
If we want to completely remove or null the interference at 60 degree angle and preserve completely the 0 degree angle, we are forcing the following,

$g\left(w,\theta=0\right)=1$

$g\left(w,\theta=60\right)=0$

The shown beam pattern has the maximum gain at 0 degree and close to zero gain at 60 degree.

Expanding the spatial gain function, we have,

$\ \ \sum_{m=1}^{M}\sum_{l=0}^{L-1}{w_{m,l}\left(l\right)\ =\ 1}$

$\sum_{m=1}^{M}\sum_{l=0}^{L-1}{w_{m,l+t_{60}}\left(l\right)\ =\ 0}$

for linear array. However this requires us to know the direction information of the interference and such information is usually unavailable in practice. Instead we can implement the following iterative algorithm without the interference information,

${min}\ {E}\left[\left|{y}\left(t\right)\right|^2\right]$

$subject\ to:g\left(w,\theta=0\right)=1$

where $y\left(t\right)=\sum_{m=1}^{M}{w_m\ast x_m\left(t\right)}$

The gradient decent iterative procedure can be realized as,

$w\left(n+1\right)=w\left(n\right)-\mu\frac{y\left(n\right)x_B\left(n\right)}{\left|y\left(p\right)\right|^2}$

with all the standard NLMS parameters. The main difference is the $x_B\left(n\right)\$ is in the orthogonal space of the desired direction.

Complete Communications Engineering