Compressive sampling array

Massive multiple-input multiple-output (MIMO) is regarded as the most significant technique in the fifth generation (5G) communications by employing a high number of antennas at the base station. Besides communication applications, massive MIMO is also appealing for the source localization due to its large array aperture. Nevertheless, it is challengeable to equip a dedicated radio frequency (RF) front-end chain and a high-resolution analog-digital converter (ADC) for each antenna in massive MIMO systems. The computational complexity is another major concern due to high-dimensional matrix operations. To address these issue, compressive sampling is an effective and feasible solution in massive MIMO systems, as Fig. 1 shows.

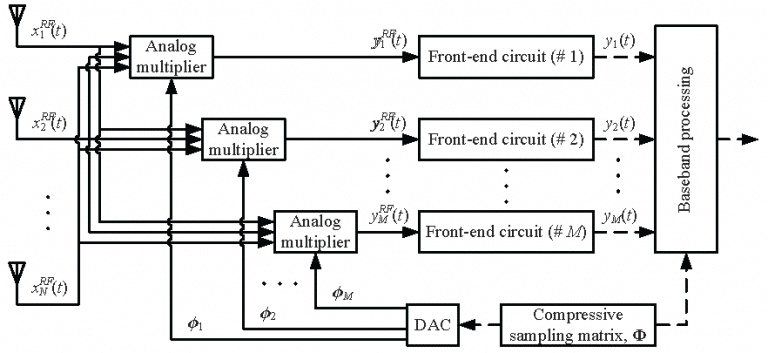
Fig. 1. Block diagram of the compressive sampling array.

In specific, we measure $M \ll N$ linear projections of the array received signal, $\boldsymbol{x}^{RF}(t)$ , onto a set of measurement kernels $\{{ \boldsymbol{\phi}_{m}, m = 1,\cdots, M}\}$ , where $M$ and $N$ respectively denote the number of measurements and the number of antennas. The $m$ -th measurement $\boldsymbol{y}^{RF}(t)$ is the projection of $\boldsymbol{x}^{RF}(t)$ onto the $m$ -th measurement kernel $\boldsymbol{\phi}_{m}$ , as

$\boldsymbol{y}^{RF}(t) = \sum_{n=1}^{N} \boldsymbol{\phi}_{m,n} \boldsymbol{x}_{n}^{RF}(t), \nonumber$

where $\boldsymbol{\phi}_{m} = \left[ \phi_{m,1}, \phi_{m,2}, \cdots, \phi_{m,N}\right]$ is the discrete representation of the analog measurement kernels.
Stacking $M$ measurement kernels as a compressive sampling matrix $\boldsymbol{\Phi} = \left[\boldsymbol{\phi}_{1}^{T}, \boldsymbol{\phi}_{2}^{T}, \cdots, \boldsymbol{\phi}_{M}^{T} \right]^{T}$ yields an $M$ -dimensional compressed measurement vector as

$\boldsymbol{y}(t) = \boldsymbol{\Phi} \boldsymbol{x}(t) = \boldsymbol{\Phi} \boldsymbol{A}(\theta) \boldsymbol{s}(t) + \boldsymbol{\Phi} \boldsymbol{n}(t),$

where $\boldsymbol{\Phi} \boldsymbol{A}(\theta) = \left[ \boldsymbol{\Phi} \boldsymbol{a}(\theta_{1}), \boldsymbol{\Phi}\boldsymbol{a}(\theta_{2}), \cdots, \boldsymbol{\Phi} \boldsymbol{a}(\theta_{D}) \right]$ is a compressed array manifold matrix with a significantly reduced dimension because $M \ll N$ . Here, $\boldsymbol{a}(\theta_{d})$ denotes the steering vector of the $d$ -th user with the direction-of-arrival (DOA) $\theta_{d}$ , $\boldsymbol{s}(t) = \left[ s_{1}(t), s_{2}(t), \cdots, s_{D}(t) \right]^{T}$ represents the signal waveform vector, and $\boldsymbol{n}(t)$ represents the zero-mean additive white Gaussian noise (AWGN) vector.

According to the compressive sensing theory, the compressive sampling matrix $\boldsymbol{\Phi}$ can be chosen a random one, e.g., Gaussian matrix or Bernoulli matrix. As such, from the compressed measurement vector $\boldsymbol{y}(t)$ over time, different array signal processing algorithms can be applied.
As we mentioned above, the required RF chains and ADCs are reduced greatly, and the computational complexity is also reduced due to the lower dimensional measurement matrix $E{\boldsymbol{y}(t) \boldsymbol{y}^{\mathrm{H}}(t)}$ .

Product Offerings
VOCAL Technologies offers custom designed, compressive sampling solutions in 5G systems. Our custom implementations of such systems are meant to deliver optimum performance for your compressive sampling tasks. Contact us today to discuss your solution!

Complete Communications Engineering

Compressive sampling array