Knowledge enhanced compressive radar ranging
In the era of 5G, faster network connections speed up the development of self-driving cars. For the self-driving cars, the key point to success is high resolution ranging/imaging. In general, automobile radars transmit wideband signals for high range resolution. According to Nyquist sampling theorem, consequently, the radar receiver requires to adopt high-rate analog-to-digital converter (ADC). In most cases, the high-rate ADCs and corresponding hardware are costly and power consumption. For example, in order to increase sampling rate by a factor of 10, the ADC would consume about 7.5 times more power and increase cost by a factor of approximately 35.
How to obtain the high resolution with a low-rate ADC? Compressive sensing (CS). The success of CS is based on two principles: sparsity and incoherence. It is well known that random sensing kernels, e.g., Gaussian and Bernoulli kernels, satisfy the incoherence requirement with signal sparse representation. However, besides sparsity, random sensing does not exploit any prior knowledge that may be available in specific applications. In automobile radar, the interested range is from 0 meter to 200 meters, which can be utilized for CS kernel optimization.
We adopt the mutual information maximization criterion to optimize the CS kernel for range estimation. The optimization problem can be formulated as
where the optimization variable is the compressive measurement matrix, and
is the mutual information between the measurement vector
and the range
. Here,
denotes the differential entropy of the measurement
,
denotes the conditional differential entropy of the measurement
conditioned on the range
, respectively. With custom defined constraints, we provide the best solution to the CS kernel optimization.
Simulation
In our simulations, the ADC is assumed to be operating at a fixed sampling rate of MHz. The radar transmit waveform is of bandwidth
MHz, where
is the compression ratio of the CS radar receiver. Meanwhile, a 1-MHz waveform is also adopted for the baseline Nyquist result, which waveform bandwidth is matched to the receiver sampling rate.
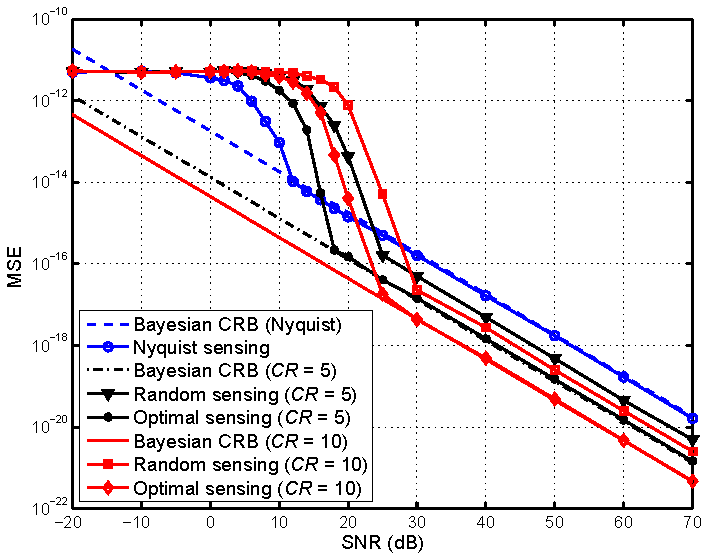
It can be observed from Fig. 1 that the optimized sensing kernel outperforms the random sensing kernels, especially at intermediate and high input SNR. In addition, it also shows that once the input SNR is sufficient (e.g., above 20 dB), performance of the compressively sampled high-bandwidth waveforms is improved over the low-bandwidth Nyquist sampling.
Product Offerings
VOCAL Technologies offers custom designed low-cost high-resolution range solutions in 5G self-driving cars. Our custom implementations of such systems are meant to deliver optimum performance for your specific range measurement task. Contact us today to discuss your solution!